PROGRAMAÇÃO, QUARTA – FEIRA, 05 DE ABRIL DE 2023
Horário: 14:00 – 14:40
Speaker : Enrique Fernandez Cara – Universidad de Sevilla, (Spain)
Title: On the control of fluids
Abstract: The Navier-Stokes equations have been studied since many years. They are very relevant in mathematics and physics and many people have been concerned with the solution of several related major open problems. On the other hand, the control of PDE’s has attracted a lot of work the last decades. This has been motivated by its very relevant role in applications. This talk is mainly devoted to present some recent results dealing with the local and global control of systems of the Navier-Stokes kind. Additionally, we will consider other equations and systems with origin in fluid mechanics.
Horário: 14:50 – 15:30
Speaker: Manuel A. Sánchez – Pontificia Universidad Católica de Chile, (Chile)
Title: Combining finite element space-discretizations with symplectic time-marching schemes for linear Hamiltonian systems
Abstract: We provide a short introduction to the devising of a special type of methods for numerically approximating the solution of Hamiltonian partial differential equations. These methods use Galerkin space-discretizations which result in a system of ODEs displaying a discrete version of the Hamiltonian structure of the original system. The resulting system of ODEs is then discretized by a symplectic time-marching method. This combination results in high-order accurate, fully discrete methods which can preserve the invariants of the Hamiltonian defining the ODE system. We restrict our attention to linear Hamiltonian systems, as the main results can be obtained easily and directly, and are applicable to many Hamiltonian systems of practical interest including acoustics, elastodynamics, and electromagnetism. After a brief description of the Hamiltonian systems of our interest, we provide an introduction to symplectic time-marching methods for linear systems of ODEs which does not require any background on the subject. Finally, we consider the case of finite-element space discretizations. The emphasis is placed on the conservation properties of the fully discrete schemes. We end by describing ongoing work.
PROGRAMAÇÃO, QUARTA – FEIRA, 22 DE MARÇO DE 2023
Horário: 14:00 – 14:40
Speaker : Juan Luis Vazquez – Universidad Autónoma de Madrid Real Academia de Ciências – Spain
Title: Nonlinear Diffusion Equations driven by Fractional Operators. Semigroups, self-similarity and asymptotics
Abstract: We will review some basic models of nonlinear diffusion driven by nonlocal operators. Then we will present some lines of recent progress in the study of p-Laplacian evolution equations both of local or nonlocal type. Existence, regularity, self-similar solutions and asymptotic behaviour are discussed.
Reading reference.
MR3588125 Vázquez, Juan Luis
The mathematical theories of diffusion: nonlinear and fractional diffusion.
Nonlocal and nonlinear diffusions and interactions: new methods and directions, 205–278,
Lecture Notes in Math., 2186, Fond. CIME/CIME Found. Subser., Springer, Cham, 2017.
Horário: 14:50 – 15:30
Speaker: Eduard Feireisl – Institute of Mathematics of the Academy of Sciences of the Czech Republic – Czech Republic
Title: Analysis of open fluid systems with uncertain data
Abstract: We consider the Navier-Stokes-Fourier system with non-conservative boundary data. First, we discuss stability of (strong) solutions with respect to the data and conditional regularity problem. We show that the solutions remain regular as long as their amplitude is controlled. Next, we apply the abstract results to the problem of convergence of approximate (numerical) solutions with uncertain data. In particular, we address convergence of the stochastic collocation and the Monte-Carlo method.
PROGRAMAÇÃO, QUARTA – FEIRA, 08 DE MARÇO DE 2023
Horário: 14:00 – 14:40
Speaker : Jean Michel Coron – Laboratoire Jacques – Louis Lions, Sorbonne Université, Université de Paris, CNRS, INRIA-équipe Cage, France
Title: Controllability and stabilization of PDE control systems with crucial quadratic terms
Abstract: We are interested in the controllability and asymptotic stabilization of some nonlinear partial differential equations where the quadratic term plays a crucial role in the sense that neither the controllability nor the asymptotic stabilization holds without these terms. We show that in this case, for the controllability, one may need more time than expected by the speed of propagation to control these systems. For the stabilization, we construct explicit time-varying feedback laws which lead to exponential stabilization for the natural weighted norm.
Horário: 14:50 – 15:30
Speaker: Iván Moyano, Université Côte D’Azur (Nice, France)
Title: Uncertainty principles in control theory of PDEs
Abstract: In this talk we review some classical and recent results relating the uncertainty principles for the Laplacian with the controllability and stabilisation of some linear PDEs. The uncertainty principles for the Fourier transforms state that a square integrable function cannot be both localised in frequency and space without being zero, and this can be further quantified resulting in unique continuation inequalities in the phase spaces. Applying these ideas to the spectrum of the Laplacian on a compact Riemannian manifold, Lebeau and Robbaino obtained their celebrated result on the exact controllability of the heat equation in arbitrarily small time. The relevant quantitative uncertainty principles known as spectral inequalities in the literature can be adapted to a number of different operators, including the Laplace-Beltami operator associated to C^1 metrics or some Schödinger operators with long-range potentials, as we have shown in recent results in collaboration with Gilles Lebeau (Nice) and Nicolas Burq (Orsay), with a significant relaxation on the localisation in space. As a consequence, we obtain a number of corollaries on the decay rate of damped waves with rough dampings, the simultaneous controllability of heat equations with different boundary conditions and the controllability of the heat equation with rough controls.
PROGRAMAÇÃO, QUARTA – FEIRA, 22 DE FEVEREIRO DE 2023
Horário: 14:00 – 14:40
Speaker : Tiago Roux Oliveira -State University of Rio de Janeiro UERJ, Brazil
Title: Extremum Seeking through Delays and Partial Differential Equations
Abstract: Exactly a century since its invention and first application, and more than two decades since the proof of its convergence, the extremum seeking control has been recognized as one of the most important model-free real-time optimization tools. However, until recently extremum seeking has been restricted to dynamic systems represented by connections of Ordinary Differential Equations (ODEs) and non-linear convex maps with unknown extremum points. This talk presents the first collection of results on the theory and design of extremum seeking strategies for infinite-dimensional systems governed by Partial Differential Equations (PDEs). The main ideas for the design of the Gradient-Newton methods and the stability analysis for infinite-dimensional systems will be discussed considering a wide class of parabolic and hyperbolic PDEs: delay equations, wave equation and reaction-advection-diffusion models. Moreover, engineering applications are presented, including problems of noncooperative games, neuromuscular electrical stimulation, biological reactors, oil-drilling systems and flow-traffic control for urban mobility.
Horário: 14:50 – 15:30
Speaker: Fernando A. Gallego Universidad Nacional de Colombia,Colombia
Title: Large Time Behaviour of a Generalized Dispersive Time-DelaySystem
Abstract: In this talk we study the asymptotic behavior of the solution of the time–delayed higher order dispersive
systems posed in the real line. Under suitable assumptions on the time delay coefficients we prove that the
system under consideration is exponentially stable in two different ways. First, if the coefficient of the delay
term is bounded from below by a positive constant, we use the Lyapunov approach to prove that the energy
associated to the solution of the higher order dispersive system decays exponentially. After that, we extend
this result to the case in which the coefficient of the undelayed feedback is also indefinite. Both problems are
investigated when the exponent p in the nonlinear term ranges over the interval [1, 2j) where 2j + 1 is the order
of the dispersive system.
PROGRAMAÇÃO, QUARTA – FEIRA, 08 DE FEVEREIRO DE 2023
Horário: 14:00 – 14:40
Speaker : Xavier Ros Oton – ICREA Research Professor, Universitat de Barcelona – Spain
Title: The singular set in the Stefan problem
Abstract: The Stefan problem, dating back to the XIXth century, is probably the most classical and important free boundary problem. The regularity of free boundaries in the Stefan problem was developed in the groundbreaking paper (Caffarelli, Acta Math. 1977). The main result therein establishes that the free boundary is $C^\infty$ in space and time, outside a certain set of singular points. The fine understanding of singularities is of central importance in a number of areas related to nonlinear PDEs and Geometric Analysis. In particular, a major question in such a context is to establish estimates for the size of the singular set. The goal of this talk is to present some new results in this direction for the Stefan problem. This is a joint work with A. Figalli and J. Serra
Horário: 14:50 – 15:30
Speaker: Maria J. Esteban – Directrice de recherche, CNRS & Université Paris – Dauphine – France
Title: Quantitative stability estimates for some functional inequalities
Abstract: In this talk I will present recent stability results for various functional inequalities, including Sobolev and the logarithmic Sobolev inequalities, proved recently in collaboration with J. Dolbeault, A. Figalli, R. Frank and M. Loss. These quantitative estimates, on the strongest possible norm, for the deficit of those inequalities are the first known ones, since up to now only non quantified estimates had been proved. In the case of subcritical functional inequalities or suboptimal norms for the estimates quantitative estimates have been proved in the past. But in not in the critical optimal case.
PROGRAMAÇÃO, QUARTA – FEIRA, 25 DE JANEIRO DE 2023
Horário: 14:00 – 14:40
Speaker : Wolfgang Arendt – Institute of Applied Analysis University of Ulm – Germani
Title: When does the Galerkin Approximation Converge? A Characterization and Application to Finite Elements
Abstract: Given a continuous bilinear Form a on Hilbert Space we V, and given L in V’ we consider the problem
a(u,v) = <L,v> for all v in V.
Given is also a sequence of finite dimensional spaces V_n, n in N.We describe under which conditions one can approximate the solution by the corresponding finite dimensional problems. In other words, we characterize under which conditions the Galerkin method converges. As is well-known, it suffices that the form is coercive. But we obtain a more general condition, namely essential coerciveness. And this condition is optimal if we admit arbitrary sequences of finite-dimensional subspaces. It turns out that this condition of essential coerciveness is satisfied if we consider the Poisson equation with respect to an elliptic operator. The point is that the operator may be quite arbitrary: there might be positive and negative eigenvalues,the only condition is that 0 is not an eigenvalue. We will consider a convex polygon in the plane and show that the approximation by finite elements converges, with quadratic convergence if the L^2 norm is considered.A different question is, whether some sequence of finite dimensional spaces exists (instead of all) such that the Galerkin method converges. This question is asked in a given Banach space X, and surprisingly, we find that a specific approximation property is equivalent to the convergence of some approximating sequence.
References: W. Arendt, I. Chalendar, R. Eymard: Galerkin approximation for linear problems in Banach and Hilbert spaces. IMA J. Numer. Anal. 42 (2022) 165-198.
W. Arendt, K. Urban: Partial Differential Equations. An Introduction to Analytical and Numerical Methods. Graduate Texts in Mathematics. Springer 2023.
Horário: 14:50 – 15:30
Speaker: Karl Kunisch – Institute of Mathematics Scientific Computing – University of Graz – Austria
Title: Learning-based optimal Feedback Control of Nonlinear Differential Equations
Abstract: Optimal feedback controls for nonlinear systems are characterized by the solutions to a Hamilton Jacobi Bellmann (HJB) equation. In the deterministic case, this is a first order hyperbolic equation. Its dimension is that of the statespace of the nonlinear system. Thus solving the HJB equation is a formidable task and one is confronted with a curse of dimensionality. In practice, optimal feedback controls are frequently based on linearisation and subsequent treatment by efficient Riccati solvers. This can be effective, but it is local procedure, and it may fail or lead to erroneous results. In the talk I present a learning-based technique, which provides optimal feedback laws without addressing the HJB equation directly. The feedback operators are approximated by neural networks or by a polynomial ansatz. Their convergence to the optimal feedback gains is established, and numerical results are presented. This is joint work with D.Vasquez and D.Walter.
PROGRAMAÇÃO, QUARTA – FEIRA, 11 DE JANEIRO DE 2023
Speaker : Alessandro Astolfi – College Consul for Faculty of Engineering and Business School Imperial College London – United Kingdom
Title: The curse of linearity and time-invariance
Abstract: The study of linear systems theory without exploiting linearity and time-invariance may pose challenges, yet it is highly rewarding. In truth, linearity and time-invariance, albeit powerful, are a curse: they are not conducive to an abstract understanding of concepts, tools and ideas and may often be misleading. On the other hand, notions such as manifold invariance, interconnection, coordinates transformations, decomposition, and the principle of optimality facilitate the enhancement of linear, time-invariant, systems theory methods and tools to far more general classes of systems. We illustrate this perspective by providing abstract and geometric definitions for eigenvalues, poles, moments, Loewner operators and derivative, and persistence of excitation; and by solving interpolation problems, adaptive and robust control problems, and optimal control and game theory problems, for general classes of nonlinear systems.
Horário: 14:50 – 15:30
Speaker: Bingyu Zhang Department of Mathematical Sciences University of Cincinnati – USA
Title: On Some Joint Effects of Dispersion and Dissipation of a Class of Nonlinear Evolution Equations
Abstract: It is known that the solutions of the Cauchy problem of the Korteweg-de Vries (KdV) equation
\[ u_t +uu_x +u_{xxx} =0, \quad u(x,0)= \phi (x), \quad x\in \T, \ t\in \R,\] and the viscous Burgers equation
\[ u_t +uu_x – u_{xx} =0, \quad u(x,0)= \phi (x), \quad x\in \T, \ t>0 \] posed on a periodic domain $\T$, {\bf do not possess } the sharp Kato smoothing property: \[ \phi \in H^s (\T) \implies \partial ^{s+1}_xu \in L^{\infty}_x (\T, L^2 (0,T)),\] %nor the Kato smoothing property, % \[ \phi \in H^s (\T) \implies u\in L^2 (0,T; H^{s+1} (\T)).\] In this talk, we will consider the Cauchy problem of following equation, \[ u_t +uu_x +\alpha (x,t) u_{xxx} – \beta (x,t)u_{xx} =0, \qquad u(x,0)= \phi (x), \quad x\in \T, \ t\geq 0, \, \] and demonstrate that if $$\int _{\mathbb{T}}\frac{\beta (x,t)}{\alpha (x,t)|} dx >0 \quad \forall t\geq 0,$$
% is locally well-posed in the space $ H^s (\T)$ with $s \geq 0$. then its solution $u$ possesses the sharp Kato smoothing property, \[ \phi \in H^s (\T) \implies \partial ^{s+1}_xu \in L^{\infty}_x (\T, L^2 (0,T)), \quad \forall \, s\geq 0. \] In addition, the nonlinear part of its solution $u$ possesses {\em the strong Kato smoothing property}, \[ \phi \in H^s (\T) \implies (u -v)\in C([0,T]; H^{s+1} (\T)), \quad \forall \, s>\frac12, \] and the {\em double sharp Kato smoothing property}, \[ \phi \in H^s (\T) \implies \partial ^{s+2}_x(u -v)\in L^{\infty}_x (\T, L^2 (0,T)), \quad \forall \, s>\frac12, \] with $ v$ being the solution of the linear problem \[ v_t+ \alpha (x,t)v_{xxx} – \beta (x,t) v_{xx} =0, \quad v(x,0)=\phi (x), \quad x\in \T, \ t>0. \]
This is a joint work with Shuming Sun, Xin Yang and Ning Zhong.
PROGRAMAÇÃO, QUARTA – FEIRA, 14 DE DEZEMBRO DE 2022
Speaker : Serena Dipierro – Department of Mathematics and Statistics, University of Western – Australia
Title: Nonlocal capillarity theory
Abstract: We present a fractional version of the classical Gauss free energy functional used in capillarity theory which takes into account surface tension energies of nonlocal type. The case of interaction kernels that are possibly anisotropic and not necessarily invariant under scaling can be also taken into account, and in this general setting we determine a nonlocal Young’s law for the contact angle and discuss the unique solvability of the corresponding equation in terms of the interaction kernels and of the relative adhesion coefficient.
Horário: 14:50 – 15:30
Speaker: Obidio Rubio Mercedes – Departamento de Matemáticas Universidad Nacional de Trujillo – Peru
Title: Non-linear Dynamical Systems: Applications
Abstract: We present an overview of results on non-linear dynamical system developed in collaboration with researchers on Hausdorff dimension of functionally invariant sets and approximate inertial manifolds on weakly viscoelastic fluid flows together with some numerical simulations and magnetohydrodynamic equations with thermal dispersion, also we see some concepts of the pullback attractors on semi linear parabolic equations.
PROGRAMAÇÃO, QUARTA – FEIRA, 30 DE NOVEMBRO DE 2022
Horário: 14:00 – 14:40
Speaker : Roberto Triggiani – Department of Mathematical Sciences University of Memphis – USA
Title: Uniform stabilization of the Boussinesq system in Besov spaces of low regularity by a localized, finite dimensional feeback controller pair {boundary, interior}
Abstract: The presentation will be based on paper [1], which in turn is stimulated by paper [2] and requires, in particular,
the contributions of [3] and [4]. The Boussinesq system on a 3d-bounded domain couples the Navier-Stokes equations with a suitable diffusion equation. One assumes at the start that the linearized version has an unstable equilibrium solution. One then constructs explicitly a static, finite dimensional pair {v, u} of feedback controllers that exponentially stabilizes the original non-linear system in the vicinity of the unstable equilibrium solution, in the uniform norm of a suitable Besov-space of low regularity, with tight indeces. Here, v is a scalar Dirichlet boundary control for the thermal equation, acting on an arbitrarily small connected component of the boundary. Instead, u is (d-1)-internal control [(d-1) is a novelty due to the B’s model] for the fluid equation acting on an arbitrarily small interior collar supported by the boundary support of v. The case of selecting a boundary-localized control this time for the Navier-Stokes equation, as in [2], will be studied next.
SELECTED REFERENCES
[1] Finite dimensional boundary uniform stabilization of the Boussinesq system in Besov spaces by critical
use of Carleman estimate-based inverse theory (with I. Lasiecka and B. Priyasad), J. of Inverse and
Ill-posed Problems. vol. 30, no. 1, (2022) pp. 35-79.
[2] Uniform Stabilization of 3D Navier–Stokes Equations in Low Regularity Besov Spaces with Finite
Dimensional, Tangential-Like Boundary, Localized Feedback Controllers (with I. Lasiecka and B.
Priyasad), Archive of Rational Mechanics and Analysis 241, (2021), 1575–1654
[3] Maximal Lp-regularity for an abstract evolution equation with applications to closed-loop boundary
feedback control (with I.Lasiecka and B. Priyasad), Journal of Differential Equations, 294 (2021):
60–87.
[4] Unique Continuation Properties of Over-determined static Boussinesq Eigenproblems with Application
to Uniform Stabilization of Dynamic Boussinesq Systems (with X. Wan), Appl. Math. &
Optimiz 84 (2021), 2099–2146.
Horário: 14:50 – 15:30
Speaker: João Rodrigues – Universidade Federal do Pará – Brasil
Title: The method of the energy function and applications
Abstract: In this work, we establish an alternative method to find critical points of differentiable functionals defined in Banach spaces which belong to an appropriated class ($\mathcal{J}$) of functionals. Once given a functional $J$ in the class ($\mathcal{J}$), the central idea of the referred method consists in defining a suitable real function $\zeta$ of a real variable, called energy function, which is naturally associated to $J$ in the sense that the existence of real critical points for $\zeta$ guarantees the existence of critical points for the functional $J$. As a consequence, we solve some variational elliptic problems, whose associated energy functional belongs to ($\mathcal{J}$) and provide a version of the mountain pass theorem for functionals in the class ($\mathcal{J}$) that does not need to satisfy the so called Palais-Smale condition.
PROGRAMAÇÃO, QUARTA – FEIRA, 16 DE NOVEMBRO DE 2022
Horário: 14:00 – 14:40
Speaker : Shu-Ming Sun – Department of Mathematics – Virginia Tech – USA
Title: Exact theory on solitary or multi-solitary waves on water of finite depth
Abstract: The talk will give a brief discussion on the development of existence and/or stability of two- and three-dimensional solitary or multi-solitary surface waves on the water of finite depth with or without surface tension using the exact governing equations (called Euler equations). It will be shown that when the non-dimensional wave-speed and surface tension are in various regions, the Euler equations possess several different kinds of two- or three-dimensional solitary or multi-solitary wave solutions. Moreover, some stability results for these waves will be addressed such as transverse instability, spectral stability, asymptotic linear stability or conditional stability. The talk is accessible to non-experts or graduate students.
Horário: 14:50 – 15:30
Speaker: Cesar Niche Mazzeo – Universidade Federal de Rio de Janeiro – Brazil
Title: Decay in Sobolev critical space for 3D Navier-Stokes-Coriolis and Navier-Stokes equations
Abstract: Using the Fourier Splitting Method and the decay character of initial data, we obtain decay rate of solutions to the 3D Navier-Stokes-Coriolis and 3D Navier-Stoke equations in the critical homogeneous Sobolev space $\dot{H}^{1/2}$. The estimates obtained are qualitatively different from those for 3D NSC and NS in $L^2$. This is joint work with Leonardo Kosloff and Gabriela Planas.
PROGRAMAÇÃO, QUARTA – FEIRA, 02 DE NOVEMBRO DE 2022
Horário: 14:00 – 14:40
Speaker : Duvan Cardona Sanchez – Department of Mathematics Ghent University – Belgica
Title: Control theory for diffusion models on compact manifolds
Abstract: In this seminar, we present some new results in [A,B] about the controllability of the fractional heat equation associated with an elliptic differential operator. The classical result by Lebeau and Robianno [2], gives the null-controllability of the hat equation in the case of the Laplacian, and recently, Rousseau and Robbiano have extended this problem to the case of the bi-Laplacian. The novelty of our work is the proof of a spectral inequality for wave packets of eigenfunctions associated with an elliptic operator (and that in some sense generalizes classical results by Donelly and Fefferman (for eigenfunctions), Lebeau and Robianno, Jerison and Lebeau, and Lebeau and Zuazua, proved in the setting of the Laplacian). In contrast with the classical approaches, via Carleman estimates, we strongly make use of the theory of pseudo-differential operators. References:
[A] D. Cardona. Controllability of fractional heat equations on compact manifolds, preprint.
[B] Cardona, D., Delgado, J., Ruzhansky, M. Estimates for sums of eigenfunctions of elliptic pseudo-differential operators on compact Lie groups, preprint.
[1]. H. Donnelly and C. Fefferman, Nodal sets of eigenfunctions on Riemannian manifolds,
Invent. Math. 93, 161-183, (1988).[2]. G. Lebeau, L. Robbiano, Controle exact de l’equation de la chaleur,
Comm. Partial Diff. Equations., 20, 335–356, (1995).
[3]. D. Jerison, G. Lebeau. Nodal sets of sums of eigenfunctions.
Harmonic analysis and partial differential equations (Chicago, IL, 1996), Chicago Lectures in Math, 223-239, 1999.[4]. G. Lebeau, E. Zuazua. Null‐Controllability of a System of Linear Thermoelasticity.
Arch. Rational Mech. Anal. 141(4), 297–329, 1998.[5]. J. Le Rousseau, L. Robbiano. Spectral inequality and resolvent estimate for the bi-Laplace operator.
J. European Math. Soc., 22, 1003-1094, (2020).
Horário: 14:50 – 15:30
Speaker: Reginaldo Demarque da Rocha – Universidade Federal Fluminense – Brazil
Title: Boundary null controllability of degenerate heat equation as thelimit of internal controllability
Abstract: In this talk we will present a work where we recover the boundary null controllability for the degenerate heat equation by analyzing the asymptotic behavior of an eligible family of state-control pairs solving corresponding singularly perturbed internal null controllability problems. As in other situations studied in the literature, our approach relies on Carleman estimates and meticulous weak convergence results. However, for the degenerate parabolic case, some specific trace operator inequalities must be obtained, in order to correctly justify the passage to the limit
argument.
PROGRAMAÇÃO, QUARTA – FEIRA, 19 DE OUTUBRO DE 2022
Horário: 14:00 – 14:40
Speaker : Genni Fragnelli – Department of Ecology and Biology, Tuscia University – Italy
Title: Controllability and stabilization for a degenerate wave equation
Abstract: We consider the problem \begin{equation} \begin{cases} u_{tt} – a(x)u_{xx} -b(x)u_x=0, & (t,x) \in Q,\\ u(t, 0)= 0, &t \in [0, +\infty),\\ u(0,x)= u_0(x), \quad u_t(0,x)=u_1(x),& x \in (0, 1), \end{cases} \end{equation} \noindent where $Q=(0,+\infty) \times(0,1)$, $f \in L^2_{\text{loc}}[0, +\infty)$, $a, b\in C^0[0,1]$, $a>0$ on $(0,1]$ and $a(0)=0$. At $x=1$ we consider different boundary conditions according to the considered problem. If we are interested in a controllability problem (see $[2]$), we assume \[ u(t,1)=f(t), \quad t \in [0, +\infty);\] thus the function $f$ acts as a boundary control and it is used to drive the solution to $0$ at a given time $T$. If we are interested in the stabilization problem (see $[3]$) we consider as a boundary condition the following damping one \[ u_t(t,1)+\eta u_x(t,1)+ \beta u(t,1)=0, \quad t \in [0,+\infty),\] where $\eta$ is a given function and $\beta$ is a nonnegative constant. Clearly the presence of the drift term and the nondivergence form lead to a different setting with respect to the one in [1] and they give rise to some new difficulties. However, thanks to some suitable assumptions on the drift term, one can prove some estimates on the associated energy that are crucial to drive the solution to $0$ at time $T$ or to obtain a uniform exponential decay as $t \rightarrow + \infty$. [1] F. Alabau-Boussouira, P. Cannarsa, G. Leugering, Control and stabilization of degenerate wave equations, SIAM J. Control Optim., 2017, 55, 2052–2087 [2] I. Boutaayamou, G. Fragnelli, D. Mugnai, Boundary controllability for a degenerate wave equation in non divergence form with drift, submitted. [3] G. Fragnelli, D. Mugnai, Linear stabilization for a degenerate wave equation in non divergence form with drift, preprint.
Horário: 14:50 – 15:30
Speaker: Ademir Pastor – Imecc – Unicamp – Brazil
Title: Exact controllability for linear dispersive PDEs on a periodic domain via moment method
Abstract: We use the classical moment method to establish a simple criterion to determine if a family of linear dispersive equations on a periodic domain is exactly controllable and exponentially stabilizable in the Sobolev spaces. We apply our results to several well-known models.
PROGRAMAÇÃO, QUARTA – FEIRA, 05 DE OUTUBRO DE 2022
Horário: 14:00 – 14:40
Speaker : Nicola Bellomo – University of Granada – Spain – Politecnico of Torino – Italy
Title: Pandemics of SARS-CoV-2 and Society: A multi-scale active particles systems approach
Abstract: The pandemic initiated by the aggressive virus, i.e. the so-called SARS–CoV–2 Severe Acute Respiratory Syndrome, corona virus n.2 has generated a tremendous impact on our society affecting health, economy, and social interactions. Researchers have been asked to provide tools to contrast the aforementioned impact. Mathematics has been involved to develop tools suitable to move beyond the deterministic approach of population dynamics with the aim of providing a multiscale derivation of models with the ability not only not only to capture the complexity of evolutionary biological dynamics, but also to provide a predictive vision suitable to support the decision making of crisis managers. This Lecture is based on the approach developed in [1] within a multiscale framework accounting for the interaction of different spatial scales, from the small scale of the virus itself and cells, to the large scale of individuals and further up to the collective behavior of populations. The mathematical framework is that of the mathematical theory of active particles [2]. The Lecture pursues the objective of developing a mathematical theory of the aforementioned complex dynamics suitable to lead to a novel generation of models useful to support some aspects of the crisis that has invaded our society. The main focus refers to the in-host dynamics and vaccination programs [3] in the case of virus mulations [4].
[1] Nicola Bellomo, Richard Bingham, Mark A. J. Chaplain, Giovanni Dosi, Guido Forni, Damian A. Knopoff, John Lowengrub, Reidun Twarock, and Maria Enrica Virgillito, A Multi-Scale Model of Virus Pandemic: Heterogeneous Interactive Entities in a Globally Connected World, Mathematical Models and Methods in Applied Sciences, 30, 1591–1651, (2020). [2] Nicola Bellomo, Abdelghani Bellouquid, Livio Gibelli, and Nisrine Outada, A Quest Towards a Mathematical Theory of Living Systems, Birkh ̈auser-Springer, New York, (2017).
[3] Nicola Bellomo, Diletta Burini, and Nisrine Outada, Pandemics of Mutating Virus and Society: A multi-scale active particles approach, Philosophical Transactions, Series A, Royal Society, 380, 20210161, (2022). [4] Nicola Bellomo, Diletta Burini, and Nisrine Outada, Multiscale Models of Covid-19 with Mutations and Variants, Networks Heter. Media, 17(3), 293–310, (2022).
Horário: 14:50 – 15:30
Speaker: Adriano Alcantara – Universidade Federal de Rio de Janeiro – PPGI – Brazil
Title: Análise e simulação numérica para um equação de ondas não linear com condições de fronteira do tipo Dirichlet, Acústica e Impenetrabilidade
Abstract: Análise e simulação numérica para uma equação de ondas não linear com com condições de Dirichlet, Acústica e Impenetrabilidade. Na parte espacial, usamos o método de elementos finitos (com bases linear e quadrática) e no tempo o método de Crank-Nicolson. Para cada tempo discreto, usamos o método de Newton para resolver o sistema algébrico não linear. Ganhador do Prêmio Marco Antônio Raupp pela SBMAC em 1° lugar de melhor tese de doutorado do ano 2021.
PROGRAMAÇÃO, QUARTA – FEIRA, 21 DE SETEMBRO DE 2022
Horário: 14:00 – 14:40
Speaker : Pierre Lissy – Université Paris – Dauphine France
Title: A non-controllability result for the half-heat equation on the whole line based on the prolate spheroidal wave functions and its application to the Grushin equation
Abstract: In this talk, after recalling some basic elements of linear control theory, I will explain how one can use some special functions, the Prolate Spheroidal Wave Functiosn (PSWF), that saturate some uncertainty principle, can be used to give non-controllability results for the half-heat equation on the real line, and for the Grushin equation on the plane.
Horário: 14:50 – 15:30
Speaker: Takeo Takamahashi – Université de Lorraine – France
Title: Interaction between an incompressible viscous fluid and an elastic wall
Abstract: We consider a viscous incompressible fluid interacting with anelastic structure located on a part of its boundary. The fluid motionismodeled by the bi-dimensional Navier-Stokes system and the structurefollows the linear wave or beam equation in dimension 1 in space. Inorder to show the existence of strong solutions for the correspondingcoupled system, we study the linearized system coupling the Stokessystem with a wave/beam equation. According to the cases, thecorresponding semigroup is analytic or of Gevrey class.
PROGRAMAÇÃO, QUARTA – FEIRA, 07 DE SETEMBRO DE 2022
Horário: 14:00 – 14:40
Speaker : Panagiotis E. Souganidis – Department of Mathematics – The University of Chicago – USA
Title: Deterministic surface growth models
Abstract: This talk is about the asymptotic behavior of large classes of (hyperbolically and parabolically) scaled deterministic surface growth models that are monotone and equivariant under translations by constants, The limits are solutions of degenerate elliptic partial differential equations which typically are discontinuous in some gradient directions consistent with Finsler metrics, such as the crystalline infinity Laplacian.
Horário: 14:50 – 15:30
Speaker: Mikhail Victor Klibanov – Department of Mathematics and Statistics – University of North Carolina at Charlotte – USA
Title: Globally Convergent Numerical Methods for Coefficient Inverse Problems of Army Needs
Abstract: Siince the field of Inverse Problems is an applied one, then it is necessary to develop reliable and rigorously justified numerical methods for coeficient inverse problems with formally determined data. Conventional numerical methods for these problems are relying on optimization of least squares cost functionals of the Tikhonov type. However, these functionals are non convex and thus, typically suffer from the problem of multiple local minima. Since any gradient-like optimization method stops at the point of a local minimum, then any conventional numerical method requires a good first guess for the solution. However, such a guess is rarely available in applications.
This talk will be focused on a new concept of numerical methods for coeficient inverse problems. This is the so-called convexification concept. The speaker has first proposed this concept in two publications [1,2] in 1995 and 1997. While initially this was only a theoretical development, starting from 2017 a number of works was published, which combine both the theory and numerical studies of the convexification, including the cases of experimental data [3], see the book [4] for a summary of these results.
The convexification amounts to the construction of a globally strictly convex cost functional for a coeficient inverse problem. The unique global minimizer of this functional exists, it is close to the true solution and it can be obtained by the gradient descent
method. This method can start from an arbitrary point. Corresponding analytical and numerical results will be presented.
- M. V. Klibanov and O. V. Ioussoupova, Uniform strict convexity of a cost functional for three-dimensional inverse scattering problem, SIAM J. Math. Anal., 26, 147-179, 1995.
- M.V. Klibanov, Global convexity in a three-dimensional inverse acoustic problem, SIAM J. Math. Anal., 28, 1371-1388, 1997.
- V. A. Khoa, G. W. Bidney, M. V. Klibanov, L. H. Nguyen, A. Sullivan, L. Nguyen, and V. N. Astratov, ConvexiÖcation and experimental data for a 3D inverse scattering problem with the moving point source, Inverse Problems, 36, 085007, 2020.
- M. V. Klibanov and J. Li, Inverse Problems and Carleman Estimates: Global Uniqueness, Global Convergence and Experimental Data, De Gruyter, 2021.
PROGRAMAÇÃO, QUARTA – FEIRA, 24 DE AGOSTO DE 2022
Horário: 14:00 – 14:40
Speaker : Robert Lipton – Department of Mathematics &Center for Computation and Technology Louisiana State University-USA
Title: Nonlocal Methods for Capturing Dynamic Fracture and Extreme Deformations
Abstract: The fracture of brittle solids is a particularly interesting collective interaction connecting both large and small length scales. Apply enough stress or strain to a sample of brittle material and one eventually snaps bonds at the atomistic scale leading to fracture of the macroscopic specimen. In this talk a nonlocal mesoscopic fracture model is presented in which fractures emerge from the initial boundary value problem as part of the solution. The nonlocal model carries details of the process zone seen at the mesoscopic length scale. In the limit of vanishing nonlocality, solutions of the model converge to solutions of the wave equation with evolving boundary formulated in Dal Maso and Toader (J. Diff. Equ. 2019). The classic Kinetic relation linking crack velocity to elastic energy flux flowing into the crack tip is recovered in the limit of vanishing nonlocality. The nonlocal dynamic initial value problem implicitly encodes the features of the classic model and delivers them in the limit of vanishing nonlocality. The mesoscopic model eleminates the need for separate mathematical treatment of crack and intact material seen in classic (macroscopic) fracture models.
Horário: 14:50 – 15:30
Speaker: Eduardo Hernandez – Departamento de Computação e Matemática, Universidade de São Paulo, Ribeirão ̃Preto-Brazil
Title: On explicit abstract neutral differential equations with state dependent delay
Abstract: We introduce and study a class of abstract neutral differential equations with state-dependent delay at the temporal derivative. We study the local and global existence and uniqueness of mild solution and the existence of strict solution. Some examples concerning partial neutral integro-differential equations are presented.
PROGRAMAÇÃO, QUARTA – FEIRA, 10 DE AGOSTO DE 2022
Horário: 14:00 – 14:40
Speaker : Aissa Guesmia – University of Lorraine, Metz, France-KFUPM, Dhahran, Kingdom of Saudi Arabia
Title: Some well-posedness and stability results forthermoelastic Bresse-type systems with different kinds of heat conduction via the vertical
Abstract: The objective of this work is to study the stability of linear one-dimensional thermoelastic Bresse-type systems in a bounded domain, where the coupling is given through the first component of the Bresse model with the heat conduction of (i) type I or (ii) type III or (iii) second sound or (iv) Gurtin-Pipkin type. We state the well-posedness and show the polynomial stability of the systems, where the decay rates depend on the smoothness of the initial data. Moreover, in cases (iii) and (iv), we prove the equivalence between the exponential stability and some new conditions on the parameters of the systems. However, in cases (i) and (ii), we prove the non-exponential stability independently of the parameters of the systems. The proof is based on the semigroup theory and a combination of the energy method and the frequency domain approach.
A part of these results was obtained in collaboration with Mounir Afilal (University of Cadi Ayyad, Morocco) and Abdelaziz Soufyane (University of Sharjah, UAE).
A part of these results was published in Applicable Analysis (2020).
Horário: 14:50 – 15:30
Speaker: Carlos Guzman Jimenez, Universidade Federal Fluminense – Brazil
Title: On the inhomogeneous nonlinear Schrodinger equation
Abstract: In this talk, we consider the Cauchy problem associated with the inhomogeneous nonlinear Schrodinger equation.We discuss the global well-posedness as well as the asymptotic behavior of the solutions. We mainly focus on the scattering problem for the intercritical and critical cases, assuming radial and non-radial initial data. The method is based on the ideas introduced by Kenig-Merle, for the critical case and Holmer Roudenko, for the intercritical setting.
This is a joint work with Luiz Farah, Jason Murphy, and Mykael Cardoso.
PROGRAMAÇÃO, QUARTA – FEIRA, 27 DE JULHO DE 2022
Horário: 14:00 – 14:40
Speaker : George Yin University of Connecticut, Storrs, CT – USA
Title: Stochastic Kolmogorov Systems and Applications
Abstract: In this talk, we present some of our recent work on stochastic Kolmogorov systems. The motivation stems from dealing with important issues of ecological and biological systems. Focusing on environmental noise, we aim to address such fundamental questions: “what are the minimal conditions for long-term persistence of a population, or long-term coexistence of interacting species”. Some optimal control problems are also examined.
[The talk reports some of our joint works with D.H. Nguyen, N.T. Dieu, N.H. Du, and N.N Nguyen.]
Horário: 14:50 – 15:30
Speaker: Wladimir Neves Universidade Federal do Rio de Janeiro – Brazil
Title: Nonlocal-fractional theory and applications to PDEs
Abstract: The theory of nonlocal operators, in particular the fractional Laplacian, has attracted great attention and has had a significant development in recent years. In this talk, we present some interesting problems related to fractional evolution equations mostly posed in bounded domains and also some systems of fractional partial differential equations, which we have worked on.
PROGRAMAÇÃO, QUARTA – FEIRA, 13 DE JULHO DE 2022
Horário: 14:00 – 14:40
Speaker : Christiane Tammer – Martin Luther – University Halle – Wittenberg, Faculty of Natural Sciences II, Institute of MathematicD-06099 Halle (Saale) – Germany
Title: Optimization problems with variable domination structures: Variational principles and applications
Abstract: In this talk, we are dealing with vector optimization problems in infinite-dimensional spaces where the solution concept is given by variable domination structures. Vector optimization with variable domination structures is a growing up and expanding field of applied mathematics that deals with optimization problems where the domination structure is given by a set-valued map. Interesting and important applications of vector optimization with variable domination structure arise in economics, behavioral sciences, in portfolio management, locational analysis and radiotherapy treatment in medicine. We introduce several concepts for solutions to vector optimization problems with variable domination structures and show corresponding characterizations by means of nonlinear functionals. Furthermore, we derive variational principles, existence results of Takahashi’s type, duality assertions, and necessary conditions for approximate solutions using techniques from variational analysis. These results are useful for further research on the field of vector optimization with variable domination structure, especially, for deriving numerical procedures. (joint work with Truong Q. Bao, Boris S. Mordukhovich and Antoine Soubeyran)
Horário: 14:50 – 15:30
Speaker: Felipe Chaves Universidade Federal de Paraíba UFPB – Brasil
Title: Switching controls for parabolic systems
Abstract: In this talk, we present some recent results on switching controls for parabolic systems. More precisely, we will consider the following problem: assuming that one can control a system using two or more actuators, does there exist a control strategy such that at all times, only one actuator is active?
PROGRAMAÇÃO, QUARTA – FEIRA, 29 DE JUNHO DE 2022
Horário: 14:00 – 14:40
Speaker : Christophe Prieur Univ. Grenoble Alpes, CNRS, Gipsa-lab Grenoble, France
Title: Stabilization of (nonlinear) PDE by means of nonlinear boundary controls
Abstract: In this presentation, the focus will be done on the design of boundary controls for distributed parameter systems as those described by linear and nonlinear partial differential equations. Saturated controllers will be discussed in this talk as those modeling feedback laws in presence of amplitude constraints. We will review some techniques for the stability analysis and the derivations of design conditions for various PDEs as parabolic and hyperbolic ones. An application in nuclear fusion will conclude this lecture.
Horário: 14:50 – 15:30
Speaker: Felipe Wergete Universidade Federal de Pernambuco UFPE-Brazil
Title: Decaimento Temporal para as Equações Magneto-Micropolares
Abstract: Nesta palestra, abordaremos o comportamento das soluções globais fracas das equações magneto-micropolares para tempos grandes. Além disso, mostraremos que a velocidade micro-rotacional decai mais rapidamente do que a velocidade linear do fluido.
PROGRAMAÇÃO, QUARTA – FEIRA, 15 DE JUNHO DE 2022
Horário: 14:00 – 14:40
Speaker : Vicentiu Radulescu – AGH University of Science and Technology, Krakow, Poland. – University of Craiova, Romania – Institute of Mathematics of the Romanian Academy, Bucharest
Title: New phenomena in the study of double-phase problems
Abstract: We study some nonstandard phenomena associated with the analysis of two classes of stationary double-phase problems. We first discuss a striking discontinuity property of the spectrum in the isotropic case. Next, we consider the anisotropic case associated with the presence of several variable exponents. In this abstract setting, we study a class of problems with mixed “subcritical-critical-supercritical” regime and we establish sufficient conditions for the existence of solutions in the radial, nonradial and singular cases. Several perspectives are developed in the final part of this talk.
Horário: 14:50 – 15:30
Speaker: Alberto Mercado – Departamento de Matemática, Universidad Técnica Federi
Title: Carleman estimates for transmission wave equations with non-convex interfaces
Abstract: We study a wave equation acting in an open bounded subset of R2 where the wave speed is assumed to be constant in each one of two sub-domains, separated by a smooth and possibly non-convex interface. We deal with the construction of Carleman weights for the wave operator, allowing gener- alizations of previous results to the case of an interface that is not necessarily the boundary of a convex set. Indeed, using the orthogonal projection onto this interface, we define convex functions satisfying the transmission conditions imposed by the equation, such that, under some hypothesis on the sign of the jump of the wave speed, can be used as Carleman weights. We also present a generalization to the general case of n dimensions and applications to the inverse problem of recovering a space-dependent potential of the equation. Joint works with Lucie Baudouin (LAAS-CNRS, France), Pamela Godoy (DMAT, Universidad Técnica Federico Santa Maria, Chile) and Axel Osses (CMM, U de Chile).
PROGRAMAÇÃO, QUARTA – FEIRA, 01 DE JUNHO DE 2022
Horário: 14:00 – 14:40
Speaker : Andrea Mondino – University of Oxford – United Kingdom
Title: Optimal transport and quantitative geometric inequalities
Abstract: The goal of the talk is to discuss a quantitative version of the Levy- Gromov isoperimetric inequality (joint with Cavalletti and Maggi) as well as a quantitative form of Obata’s rigidity theorem (joint with Cavalletti and Semola). Given a closed Riemannian manifold with strictly positive Ricci tensor, one estimates the measure of the symmetric difference of a set with a metric ball with the deficit in the Levy- Gromov inequality. The results are obtained via a quantitative analysis based on the localisation method via L1-optimal transport. For simplicity of presentation, the talk will present the results in case of smooth Riemannian manifolds with Ricci Curvature bounded below; moreover it will not require previous knowledge of optimal transport theory.
Horário: 14:50 – 15:30
Speaker: Ivonne Rivas Triviño – Universidad del Valle – Colômbia
Title: Controllability of the Boussinesq Equation
Abstract: The Boussinesq equation ytt + yxxxx + yxx + yyx = 0, models water waves on a shallow channel. From the mathematical point of view can be fixed as a dispersive equation, which has been very well studied. Ana-
lytically, by [7, 4, 5, 9, 10] and also from control theory by [8, 3, 2]. In this talk, the Boussinesq equation will be presented analyzing the well-posedness and controllability of the equation when it is set in a different domain. Showing some properties and difficulties of the equation. As well as some generalization of the main operator and some ideas of how it could be addressed for future work.
PROGRAMAÇÃO, QUARTA – FEIRA, 18 DE MAIO DE 2022
Horário: 14:00 – 14:40
Speaker : Lionel Rosier – Université du Littoral Côte d’Opale (ULCO) – France
Title: Numerical control of the wave equation by a direct approach
Abstract: We are concerned with the numerical exact controllability of the linear or semilinear wave equation on the interval (0,1). We introduce a Picard iterative scheme yielding a sequence of approximated solutions which converges towards a solution of the null controllability problem, provided that the initial data are small enough. For the linear part, the control input is obtained by imposing a transparent boundary condition at x=1. Next, we provide several simulations to show the efficiency of the algorithm, using collocation pseudospectral methods on Chebychev grids to discretize the second order derivative in space in the wave equation. Some (partial) extension to the dimension 3 will also be discussed. This is a joint work with Marcelo Cavalcanti, Valeria Domingos Cavalcanti and Carole Rosier.
Horário: 14:50 – 15:30
Speaker: Ana Leonor Silvestre – Instituto Superior Técnico, Universidade de Lisboa – Portugal
Title: Navier-Stokes flows around moving obstacles
Abstract: Consider a rigid body moving through a Navier-Stokes liquid which fills the three-dimensional domain exterior to the solid, and the steady state regime of the system body-liquid, as seen by an observer attached to the solid. In this seminar, we will see what is the role of the generalized Oseen fundamental solution in the derivation of precise information about the asymptotic behavior of the velocity and pressure of the fluid. This is crucial to obtain the integrability properties of solutions and allows to justify rigorously the validity of the energy equation and the formation of a wake region behind the solid. Other physically relevant problems, where information about the asymptotic structure of the solution is important, include stability of stationary motions, characterization of flows with finite kinetic energy and flow control in exterior domains. This is based on joint works with G. P. Galdi (Univ. Pittburgh, USA), T. Takahashi (INRIA Nancy Grand-Est, France) and T. Hishida (Nagoya University, Japan).
PROGRAMAÇÃO, QUARTA – FEIRA, 04 DE MAIO DE 2022
Horário: 14:00 – 14:40
Speaker : Sophie Tarbouriech – LAAS-CNRS – Université de Toulouse; CNRS, Toulouse – France
Title: Some ingredients on event-triggered control for some partial differential equations
Abstract: Event-triggered control devises event-triggering mechanisms leading to only seldom control updates. In event-triggered control, two objectives are (1) emulation, whereby the controller is a priori predesigned and only the event-triggering rules have to be designed and (2) co-design, where the joint design of the control law and the event-triggering conditions has to be performed. Control systems are connected to generic digital communication networks for implementation, transmission, coding, or decoding. Therefore, event-triggered control strategies have been developed to cope with communication, energy consumption, and computation constraints. The talk is within this scope when dealing with some partial differential equations. Indeed, this talk proposes condition to carry out the global exponential stability of the wave equation under an event-triggering mechanism that updates a damping source term. The damping is distributed in the whole space but sampled in time. The well-posedness of the closed-loop event-triggered control system is considered. The talk mainly focuses on the avoidance of Zeno behavior provided that the initial data are more regular. The interest of the results is drawn through some numerical simulations.
Horário: 14:50 – 15:30
Speaker: Nicolás Carreño – Departamento de Matemática Universidad Técnica Federico Santa María – Chile
Title: Internal null controllability of the generalized Hirota-Satsuma system
Abstract: The generalized Hirota-Satsuma system consists of three coupled nonlinear Korteweg-de Vries equations. By using two distributed controls it is proven that the local null controllability property holds when the system is posed on a bounded interval. First, the system is linearized around the origin obtaining two decoupled subsystems of third order dispersive equations. This linear system is controlled with two inputs, which is optimal. This is done with a duality approach and some appropriate Carleman estimates. Then, by means of an inverse function theorem, the local null controllability of the nonlinear system is proven. Joint work with Emmanuelle Crépeau (Université Grenoble Alpes) and Eduardo Cerpa (Pontificia Universidad Católica de Chile).
PROGRAMAÇÃO, QUARTA – FEIRA, 20 DE ABRIL DE 2022
Horário: 14:00 – 14:40
Speaker : Piermarco Cannarsa – Dipartimento di Matematica – Universita di Roma “Tor Vergata” – Roma, Italy
Title: Scalar-input bilinear control problems for evolution equations
Abstract: Bilinear control systems are receiving increasing attention in recent years, as they can be used to study problems for which an additive control action would be unrealistic. For such systems, in infinite dimension, weaker controllability properties can be expected than for systems with additive controls. Even more so when attention is restricted to scalar-input controls, that is, controls given by scalar functions depending only on time. Even though exact controllability is out of question – due to a negative result by Ball, Marsden, and Slemrod back in the 80’s – one can still seek to steer states to special targets, or keep the energy of solutions at a constant level. This talk will present recent results for evolution equations of the form u'(t) = Au(t) + p(t)Bu(t), as well as applications to diffusive systems.
Horário: 14:50 – 15:30
Speaker: Damião J. Araújo – Department of Mathematics – Universidade Federal da Paraíba – UFPB – Brazil
Title: Improved regularity estimates for degenerate fully nonlinear elliptic equations
Abstract: We will discuss interior versus boundary regularity estimates of viscosity solutions to degenerate fully nonlinear elliptic PDEs. We will be interested in showing how (precisely) the smoothness of a given solution is affected by the degenerate diffusion model and its boundary datum.
PROGRAMAÇÃO, QUARTA – FEIRA, 06 DE ABRIL DE 2022
Horário: 14:00 – 14:40
Speaker : Manuel del Pino – University of Bath – United Kingdom
Title: Dynamics of concentrated vorticities in 2d and 3d Euler flows
Abstract: A classical problem that traces back to Helmholtz and Kirchhoff is the understanding of the dynamics of solutions to the Euler equations of an inviscid incompressible fluid when the vorticity of the solution is initially concentrated near isolated points in 2d or vortex lines in 3d. We discuss some recent results on these solutions’ existence and asymptotic behavior. We describe, with precise asymptotics, interacting vortices, and traveling helices. We rigorously establish the law of motion of ”leapfrogging vortex rings”, initially conjectured by Helmholtz in 1858
Horário: 14:50 – 15:30
Speaker: Kévin Le Balc’h – Institut de Mathématiques de Bordeaux – France
Title: Observability inequalities for elliptic equations with potentials in 2D and applications to control theory
Abstract: The goal of the talk is to present new observability estimates for non homogeneous elliptic equations, posed on a domain in R^2, and observed from a subdomain. More precisely, for a real-valued bounded potential V, we show that the constant of observability of the operator −∆ + V , is of order exp(|V |_{\infty}^{1/2+ε}). The method of proof is inspired by a recent article of Logunov, Malinnikova, Nadirashvili, Nazarov dealing with the Landis con- jecture in the plane. I will present the three main ideas of the proof: a perforation process based on the nodal set of the solution that transforms the domain to a perforated domain with small Poincaré constant, a quasiconformal transformation to reduce the elliptic equation into an harmonic equation and Carleman estimates conjugated with Harnack inequalities. Finally, I will present new results for controlling semi-linear elliptic equations in the spirit of Fernandez-Cara, Zuazua’s open problem concerning small-time global null-controllability of slightly super-linear heat equations. This is a joint work with Sylvain Ervedoza.
PROGRAMAÇÃO, QUARTA – FEIRA, 23 DE MARÇO DE 2022
Horário: 14:00 – 14:40
Speaker : Maíra Aguiar. Basque Center for Applied Mathematics, BCAM, Bilbao – Spain
Title: On the origin of complex dynamics in multi-strain dengue models
Abstract: Dengue fever epidemiological dynamics shows large fluctuations in disease incidence, and several mathematical models describing the transmission of dengue viruses have been proposed to explain the irregular behavior of dengue epidemics. Multi-strain dengue models are often modeled with SIR-type models where the SIR classes are labeled for the hosts that have seen the individual strains. The extended models show complex dynamics and qualitatively a very good result when comparing empirical data and model simulations. However, modeling insights for epidemiological scenarios characterized by chaotic dynamics, such as for dengue fever epidemiology, have been largely unexplored. The problem is mathematically difficult and to make the urgently needed progress in our understanding of such dynamics, concepts from various fields of mathematics as well the availability of good data for model evaluation are needed.
In this talk, I will present a set of models motivated by dengue fever epidemiology and compare different dynamical behaviors originated when increasing complexity into the model framework.
Horário: 14:50 – 15:30
Speaker: Manuel González Burgos. Dpto. Ecuaciones Diferenciales y Análisis Numérico Universidad de Sevilla – Spain
Title: Boundary control cost for parabolic systems
Abstract: In this talk we will present new results on the cost of the boundary controllability of parabolic systems at time T > 0. In particular, we will study sharp estimates of the control cost at time T (T small enough) when the eigenvalues of the generator of the C0 semigroup accumulate and do not satisfy a gap condition. The main ingredient that we will use is the moment method.
PROGRAMAÇÃO, QUARTA – FEIRA, 09 DE MARÇO DE 2022

Horário: 14:00 – 14:40
Speaker : Claudianor Oliveira Alves Universidade Federal de Campina Grande – UFCG – Brazil
Title: On existence of multiple normalized solutions to aclass of elliptic problems in whole Rn via Lusternik-Schnirelman category
Abstract: Ver PDF
Horário: 14:50 – 15:30
Speaker: Adán J. Corcho Federal University of Rio de Janeiro – UFRJ – Brazil
Title: Stability of nonlinear patterns in low dimensional Bose gases
Abstract: In this talk we will present recent results on the study of the orbital stability properties of the simplest nonlinear pattern in low dimensional Bose gases, the black soliton solution. In the first part of the talk, we will introduce basic notions and concepts related with this quantum model as well as physical and mathematical motivations to approach that problem. In the second part of the talk, we will present a more detailed scheme of the main result of this work on stability of the black soliton. This is a solution of a one dimensional nonintegrable defocusing Schr ̈odinger model, represented by the quintic Gross-Pitaevskii equation (5GP). Once the black soliton is characterized as a critical point of the associated Ginzburg-
Landau energy of the 5GP, I will show some coercivity properties of that energy around the black (and dark) soliton. I will also explain how to impose suitable orthogonality conditions and how to control the growth of some modulation parameters to finally prove that perturbations generated by the symmetries of the 5GP stay close to the black soliton in the energy
space.
This is a joint work with Miguel Alejo, UCO/Spain.
PROGRAMAÇÃO, QUARTA – FEIRA, 23 DE FEVEREIRO DE 2022
Horário: 14:00 – 14:40
Speaker : Miroslav Krstic – University of California San Diego – Director of The Center for Control Systems and Dynamics at UC San Diego-US
Title: Positivity, Non-undershooting, Control Barrier Functions, and Safe Control of PDEs
Abstract: While control subject to state constraints is not a new topic, even for PDEs, this subject is currently receiving peak attention in nonlinear ODE control, under the title “safe control.” The motivation comes from control of driverless cars and autonomous robotics. The so-called “control barrier functions” (CBFs) and “QP safety filter design” dominate the landscape. I will present four PDE control results which represent examples of control laws designed to ensure that physical constraints of PDE systems (such as positivity of pressure or water height, concentration of a population, or the maintenance of liquid temperature above the freezing point) are guaranteed. Some of these results are connected with a backstepping design for “non-overshooting” control which I introduced in 2006, except that in these PDE examples, where the constraint is the positivity of the state, the results take the form of “non-undershooting” control. The four topics that I cover are: bioreactors, piston-gas system, water-tank transfer, and the Stefan model of phase transition. Most of the results involve moving boundaries, governed by ODEs. Some of the PDEs are hyperbolic, some parabolic, and some mixed. Most of the work is a collaboration with Iasson Karafyllis, while some of it is with Shumon Koga.
Horário: 14:50 – 15:30
Speaker: Luiz Gustavo Farah – Universidade Federal de Minas Gerais (UFMG)-Brazil
Title: Blow-up solutions of the intercritical inhomogeneous NLS equation
Abstract: We consider the inhomogeneous nonlinear Schrödinger (INLS) equation $ iu_{t} + ∆u + |x|^{−b}|u|^{2σ}u = 0 $ , x ∈ RN , with N ≥ 3 and 0 < b < min{N/2, 2}. We focus on the intercritical case, where the scaling invariant Sobolev index sc =N/2 −(2−b)/ 2σ satisfies 0 < sc < 1. In this talk, for initial data in H^{sc} ∩ H^{1}, we discuss the existence of blow-up solutions and also a lower bound for the blow-up rate in the radial and non-radial settings. This is a joint work with Mykael Cardoso (Universidade Federal do Piauí, Brasil).
PROGRAMAÇÃO, QUARTA – FEIRA, 09 DE FEVEREIRO DE 2022
Horário: 14:00 – 14:40
Speaker : Eduardo Casas Renteria – Universidad de Cantabria -Espanha
Title: Stability for Semilinear Parabolic Optimal Control Problems with respect to Initial Data
Abstract: A distributed optimal control problem for a semilinear parabolic partial differential equation is investigated. The stability of locally optimal solutions with respect to perturbations of the initial data is studied. Based on different types of sufficient optimality conditions for a local solution of the unperturbed problem, Lipschitz or Hölder stability with respect to perturbations are proved. Moreover, a particular example with semilinear equation, constant initial data, and standard quadratic tracking type objective functional is constructed that has at least two different locally optimal solutions. By the perturbation analysis, the existence of a problem with non-constant initial data is shown that also has at least two different locally optimal solutions.
Horário: 14:50 – 15:30
Speaker: Oscar Jarrin – Universidad de Concepcion – Chile
Title: Long-time asymptotics for a damped Navier-Stokes-Bardina mode
Abstract: In this talk, we consider a damped Navier-Stokes-Bardina model posed on the whole three-dimensional space. These equations arise from some oceanic model and, from the mathematical point of view, they write down as the well-know Navier-Stokes equations with an additional nonlocal operator in their nonlinear transport term, and moreover, with
an additional damping term depending of a parameter. We study first the existence and uniqueness of global in time weak
solutions in the energy space. Thereafter, we are interested in describing their long time behavior. For this, we use some tools in the theory of dynamical systems to prove the existence of a global attractor, which is compact subset in the energy space attracting all the weak solutions when the time goes to infinity. Moreover, we derive an upper bound for the fractal dimension of the global attractor associated to these equations. Finally, for a particular choice of the damping parameter, we are also able to give an acutely description of its internal structure.
PROGRAMAÇÃO, QUARTA – FEIRA, 26 DE JANEIRO DE 2022
Horário: 14:00 – 14:40
Speaker : Jose A. Carrillo – Mathematical Institute, University of Oxford, Reino Unido
Title: Nonlocal Aggregation-Diffusion Equations: entropies, gradient flows, phase transitions and applications
Abstract: This talk will be devoted to an overview of recent results understanding the bifurcation analysis of nonlinear Fokker-Planck equations arising in a myriad of applications such as consensus formation, optimization, granular media, swarming behavior, opinion dynamics and financial mathematics to name a few. We will present several results related to localized Cucker-Smale orientation dynamics, McKean-Vlasov equations, and nonlinear diffusion Keller-Segel type models in several settings. We will show the existence of continuous or discontinuous phase transitions on the torus under suitable assumptions on the Fourier modes of the interaction potential. The analysis is based on linear stability in the right functional space associated to the regularity of the problem at hand. While in the case of linear diffusion, one can work in the L2 framework, nonlinear diffusion needs the stronger Linfty topology to proceed with the analysis based on Crandall-Rabinowitz bifurcation analysis applied to the variation of the entropy functional. Explicit examples show that the global bifurcation branches can be very complicated. Stability of the solutions will be discussed based on numerical simulations with fully explicit energy decaying finite volume schemes specifically tailored to the gradient flow structure of these problems. The theoretical analysis of the asymptotic stability of the different branches of solutions is a challenging open problem. This overview talk is based on several works in collaboration with R. Bailo, A. Barbaro, J. A. Canizo, X. Chen, P. Degond, R. Gvalani, J. Hu, G. Pavliotis, A. Schlichting, Q. Wang, Z. Wang, and L. Zhang. This research has been funded by EPSRC EP/P031587/1 and ERC Advanced Grant Nonlocal-CPD 883363.
Horário: 14:50 – 15:30
Speaker: Liliane Basso Barichello – IME-Universidade Federal do Rio Grande do Sul – Brasil
Title: Soluções de Sistemas Lineares Relevantes em Modelos de Transporte de Partículas
Abstract: A discretização das variáveis que representam a direção da partícula em modelos de transporte associados com a Equação (integrodiferencial) Linear de Boltzmann, é uma técnica bastante conhecida, que determina a chamada aproximação por ordenadas discretas da equação. Resulta disso que o modelo fundamental passa a ser um sistema de equações diferenciais. Nesta conferência, introduzimos sistemas de equações lineares, de grande porte, presentes em uma solução espectral da aproximação em ordenadas discretas da equação de transporte em geometria bidimensional. Discutimos a relação das estruturas das matrizes, e consequente métodos de solução, com a escolha das direções das partículas. Apresentamos aplicações em modelos de transferência de calor por radiação em meios com espalhamento anisotrópico, de interesse, por exemplo, na modelagem da tomografia óptica.
PROGRAMAÇÃO, QUARTA – FEIRA, 12 DE JANEIRO DE 2022
Horário: 14:00 – 14:40
Speaker : Marius Tucsnak Université de Bordeaux- France
Title: Reachable states for infinite dimensional linear systems: old and new
Abstract: Determining the reachable spaces of dynamical systems is one of the major objectives un control theory. Indeed, these spaces measure our capability of influencing the state of a system. Until recently, this question has bee considered elusive in the case of systems described by PDEs. The aim of this talk is to describe some of the recent advances on this topic, with focus on systems described by the heat equation and some of its perturbations. We describe, in particular, new and surprising connections with the theory of Hilbert spaces of holomorphic functions.
Horário: 14:50 – 15:30
Speaker: Sorin Micu Universitatea din Craiova- Romania
Title: Controllability properties of a fractional diffusion equation
Abstract: We study the controllability properties of a one-dimensional fractional parabolic equation, which may serve as a mathematical model for anomalous diffusion phenomena. It is known that, if the support of the control is fixed, this equation is not even spectrally controllable. We show that, when the control support is shifted in time with constant velocity c, the system is null-controllable in a sufficiently large time depending on c.
PROGRAMAÇÃO, QUARTA – FEIRA, 15 DE DEZEMBRO
Horário: 14:00 – 14:40
Speaker : Roberto Imbuzeiro Oliveira – Instituto de Matematica Pura e Aplicada-IMPA – Brazil
Title: Processos de Markov reversíveis e seu espectro
Abstract: Processos estocásticos de Markov são aqueles que evoluem sem “memória”. Uma condição técnica chamada de reversibilidade permite que se use teoria espectral para estudar tais processos. por esta razão, o chamado “hiato espectral” é um parâmetro importante na análise destes processos. Nesta palestra, obteremos de forma sistemática alguns resultados do seguinte tipo: dados a distribuição estacionária de um processo e o seu hiato espectral, qual é o maior valor possível para um dado parâmetro de interesse? Veremos respostas a esta pergunta nos casos de tempos de chegada (quanto tempo demora até o processo visitar certo conjunto); concentração (qual a chance de se passar tempo atípico num conjunto); e tempos de encontro (quanto tempo até dois processos independentes se aproximarem). Desta forma, reprovamos alguns resultados antigos de forma mais fácil e obtemos alguns novos teoremas novos. O trabalho descrito é conjunto com Yuval Peres.
Horário: 14:50 – 15:30
Speaker: Mauricio Santos – Universidade Federal de Paraiba-UFPB – Brazil
Title: Sobre um problema de controle multiobjetivo para a equação de Kuramoto-Sivashinsky
Abstract: Nesta palestra, apresentaremos uma classe de problemas de controle multiobjetivo para equações diferenciais parciais e mostraremos alguns resultados recentes obtidos para a equação de quarta ordem de Kuramoto-Sivashinsky.
PROGRAMAÇÃO, QUARTA – FEIRA, 01 DE DEZEMBRO
Horário: 14:00 – 14:40
Speaker : Arnaud Munch – Laboratoire de Mathématiques Blaise Pascal, Université Clermont Auvergne, UMR CNRS-France
Title: Constructive exact controls for semilinear PDEs
Abstract: It has been proved by Zuazua in 1993 that the internally controlled semilinear 1D wave equation
∂tty − ∂xxy + g(y) = f1ω, with Dirichlet boundary conditions, is exactly controllable in H10 (0, 1) ∩L2(0, 1) with controls f ∈ L2((0,1) × (0, T)), for any T > 0 and any nonempty open subset ω of (0, 1), assuming that g ∈ C1(R) does not grow faster than β|r| ln2|r| at infinity for some β > 0 small enough. The clever proof, based on the Leray-Schauder fixed point theorem, is not constructive.
In this talk,
we present a constructive proof and algorithm for the exact controllability of semilinear 1D wave equations. Assuming that g0 does not grow faster than β ln2 |r| at infinity for some β > 0 small enough and that g0 is uniformly H ̈older continuous on R with exponent p ∈ [0, 1], we design a least-squares algorithm yielding an explicit sequence converging to a controlled solution for the semilinear equation, at least with order 1 + p after a finite number of iterations.
We extend the proof to the multidimensional case assuming that g0 does not grow faster than β ln1/2|r| at infinity, by using a result of Fu, Yong and Zhang in 2007.
We show that the method also applies for the (much more intricate situation of) heat equation by considering appropriate cost functional for the controlled pair of the corresponding linearized equation, depending on parametrized Carleman weights. Large enough parameters ensure the convergence of the algorithm. We end the talk by remarking that a zero order fixed point operator derived from a zero order linearization is indeed contracting for any large enough Carleman parameter. This allows notably to greatly simplified the seminal proof of controllability due to Fernandez-Zuazua in 2000.
This talk is based on a series of recent works with Arthur Bottois (Clermont-Ferrand), Sylvain Ervedoza (Bordeaux), Jerome Lemoine (Clermont-Ferrand), Ir`ene Gayte (Sevilla), Emmanuel Trelat (Sorbonne Paris).
Horário: 14:50 – 15:30
Speaker: Dilberto. Almeida Júnior – Department of Mathematics, Federal University of Pará- Brazil
Title: Estabilização de sistemas de Timoshenko do ponto de vista do segundo espectro de frequência
Abstract: Nesta palestra abordaremos recentes avanços em estabilização para versões simplificadas do modelo de Timoshenko. Mostraremos, do ponto de vista físico, que o despercebido segundo espectro de frequências possui forte impacto para a análise de estabilização dos sistemas parcialmente dissipativos.
PROGRAMAÇÃO, QUARTA – FEIRA, 17 DE NOVEMBRO
Horário: 14:00 – 14:40
Speaker : Abimael Loula – Laboratório Nacional de Computação Científica-Brazil
Title: Metodo de elementos finitos para o problema de Biot
Abstract: O desenvolvimento de métodos numéricos para problemas da poro-elasticidade é de grande interesse na mecânica computacional, pelas suas aplicações relevantes na indústria do petróleo, engenharia civil, engenharia biomédica e ciência dos materiais, por exemplo. Consideramos como modelo o problema de consolidação linear do Biot em duas dimensões espaciais. Para este modelo simples, aproximações baseadas em métodos de elementos fintos de Galerkin contínuos têm sido propostas e analisadas. É sabido que com esta formulação, certas combinações de interpolações, incluindo ordem igual para todos os campos, são instáveis, devido à restrição incompressibilidade no campo de deslocamento no instante inicial. Com o objetivo de obter mais flexibilidade na escolha dos espaços de aproximação, propomos métodos de elementos finitos híbridos estabilizados com multiplicadores de Lagrange associados aos traços dos campos de deslocamentos e de pressões. Assim, recuperamos a estabilidade para aproximações de igual ordem para todos os campos.
Horário: 14:50 – 15:30
Speaker: Marcia Federson – Universidade de São paulo-São Carlos-Brazil
Title: Semilinear parabolic PDEs as generalized ODEs.
Abstract: It is known that generalized ODEs encompass many other types of equations as ordinary and functional differential equations, impulsive and measure differential equations, dynamic equations on time scales, integral equations and stochastic differential equations. In a joint work with Fernanda Andrade da Silva and Eduard Toon, we proved that semilinear parabolic PDEs can be regarded as generalized ODEs as well. The aim of our talk is to present the main ideas on how to prove this.
PROGRAMAÇÃO, QUARTA – FEIRA, 03 DE NOVEMBRO
Horário: 14:00 – 14:40
Speaker : Yuri Saporito – School of Applied Mathematics (EMAp), Getulio Vargas Foundation (FGV) – Brazil
Title: Stochastic Control and Differential Games with Path-Dependent Influence of Controls on Dynamics and Running Cost
Abstract: In this talk we will show how to use the functional Itô calculus framework to find a path-dependent version of the Hamilton-Jacobi-Bellman equation for stochastic control problems that feature dynamics and running costs that depend on the path of the control. We will show applications of our results to path-dependence of the delay type.
Horário: 14:50 – 15:30
Speaker:Antonio Castelo Filho -Institute of Mathematics and Computational Sciences (ICMC),University of Sao Paulo (USP)-Brazil
Title: Simulação de Escoamentos Viscoelásticos Utilizando o Sistema HiG-Flow
Abstract: Nesta apresentação vamos apresentar o sistema HiG-Flow que é capaz de simular escoamentos viscoelásticos diferenciais, tais como Oldroyd-B, Giesikus, PTT, GPTT, entre outros; modelos integrais, tais como Maxwell, KBKZ.
Entre as capacidades do sistema estão a possibilidade de simular problemas com viscosidade variável, eletroosmose, e escoamentos bifásicos com quaisquer modelos viscoelásticos, além de permitir que o usuário crie simule seu próprio modelo viscoelástico sem ter que modificar o sistema.
Quanto às técnicas numéricas, o sistema permite utilizar estabilizadores numéricos do tipo Kernel-Conformation além de poder simular escoamentos puramente viscoelásticos, sem adição de solventes.
PROGRAMAÇÃO, QUARTA – FEIRA, 20 DE OUTUBRO
Horário: 14:00 – 14:40
Speaker : Celso Costa – Univerdade Federal Fluminense, Brasil
Title: Superfície Costa e a Vida Misteriosa dos Matemáticos
Abstract: Nessa palestra pretendo abordar dois desafios importantes em minha trajetória científica e literária:
a descoberta da Superfície Costa nos idos de 1982 e a recente publicação do meu livro de ficção “A Vida Misteriosa dos Matemáticos”. Sobre o livro trata-se de uma História da Matemática narrada na tradição do realismo mágico da literatura latino-americana, a partir de um lugar chamado Aleph, onde matemáticos de todos os tempos convivem simultaneamente.
Horário: 14:50 – 15:30
Speaker : Esptiben Rojas Bernilla – Universidad de Magallanes, Chile
Title: Aspectos históricos de las E.D.P.
Abstract: En esta charla daremos un paseo histórico- filosófico de la E.D.P., desde su génesis hasta el siglo XX.
Las primeras E.D.P. fueron establecidas por Isaac Newton en el S. XVII. Su estudio sistemático fue iniciado por Jean Bernoulli (1727), Leonard Euler (1734), y D’Alembert (1743), alrededor del problema de la cuerda vibrante y la ecuación del potencial (resuelta por Simon Laplace). Las E.D.P. estimuló profundos estudios sobre la teoría de funciones, cálculo de variaciones, desarrollo de series y geometría diferencial. En 1822 la Teoría Analítica del Calor de Joseph Fourier, condujo a discutir
conceptos matemáticos importantes como, el de función y convergencia. A fines del siglo XIX y principios del XX, las E.D.P.
contribuyó para el nacimientos de los primeros espacios abstractos (métricos, normados, Banach, Sóvolev etc.). Se inicia la aplicación del análisis funcional a las E.D.P. con el desarrollo de las derivadas generalizadas o débiles, y así la teoría de distribuciones. Se empieza a generalizar los problemas clásicos a un apropiado problema de análisis funcional, en busca de soluciones en el sentido generalizado en adecuados espacios de Sóvolev, además se empiezan a estudiar la regularidad de las soluciones.
PROGRAMAÇÃO, QUARTA – FEIRA, 06 DE OUTUBRO
Horário: 14:00 – 14:40
Speaker : Emmanuel Trelat – Sorbonne Université-CNRS – Université de Paris – Directeur du Laboratoire Jacques-Louis Lions – France
Title: On the turnpike property
Abstract: The turnpike property was discovered in the 50’s by the Nobel prize Samuelson in econometry. It stipulates that the optimal trajectory of an optimal control problem in large time remains essentially close to a steady state, itself being the optimal solution of an associated static optimal control problem. We have established the turnpike property for general nonlinear finite and infinite dimensional optimal control problems, showing that the optimal trajectory is, except at the beginning and the end of the time interval, exponentially close to some (optimal) stationary state, and that this property holds as well for the optimal control and for the adjoint vector coming from the Pontryagin maximum principle. We prove that the exponential turnpike property is due to an hyperbolicity phenomenon which is intrinsic to the symplectic feature of the extremal equations. We infer a simple and efficient numerical method to compute optimal trajectories in that framework, in particular an appropriate variant of the shooting method. The turnpike property turns out to be ubiquitous and the turnpike set may be more general than a single steady-state, like for instance a periodic trajectory. We also show the property of shape turnpike for PDE models in which a subdomain evolves in time according to some optimization criterion. These works are in collaboration with Gontran Lance, Can Zhang and Enrique Zuazua.
Horário: 14:50 – 15:30
Speaker : Yulia Petrova – Saint-Petersburg State University – – Instituto de Matemática Pura e Aplicada(IMPA) – Brasil
Title: Admissibilidade das descontinuidades de contato: aplicação para recuperação melhorada de petróleo
Abstract: Na palestra, discutiremos soluções de problemas de Riemann para sistemas de leis de conservação não estritamente hiperbólicos. A solução consiste em uma sequência de ondas que se propagam com certas velocidades. Devido a efeitos não lineares, as ondas podem se espalhar (formando ondas de rarefação) ou focalizar (formando ondas de choque). Será dada a atenção especial às ondas que não se espalham, nem focalizam – as chamadas descontinuidades de contato. Para que a solução seja única, é necessário encontrar um critério de admissibilidade apropriado para choques e descontinuidades de contato. Aqui, a física do problema vem em socorro, e a introdução de termos pequenos de difusão ou reação determina a solução fisicamente admissível. Consideraremos um modelo de fluxo bifásico (água com polímero e óleo) que surge em recuperação melhorada de petróleo e mostraremos como o critério de admissibilidade ad hoc de Isaacson-Glimm pode ser obtido de forma natural.
PROGRAMAÇÃO, QUARTA – FEIRA, 22 DE SETEMBRO
Horário: 14:00 – 14:40
Speaker : Patrizia Pucci – Dipartimento di Matematica e Informatica – Università degli Studi di Perugia – Italy
Title: On certain local and nonlocal (p, q) systems in RN with critical and Hardy terms
Abstract: Motivated by important applications in nonlinear elasticity, recently great attention has been devoted to the study of local and nonlocal nonlinear problems with (p, q) growth conditions. We present existence results for a class of parametric (p, q) systems with critical and Hardy terms in RN , provided that the parameter is sufficiently large. The interest is twofold: on one hand, the simultaneous presence of critical terms, Hardy terms and the fact that the systems are studied in the whole RN cause, roughly speaking, a triple loss of compactness which
dramatically affects the applicability of standard variational methods. On the other hand, since we treat both the local and the nonlocal version of the system, the comparison of the results obtained for fractional Laplacian operators with their local counterpart is noteworthy.
The results of the talk are based on joint with Letizia Temperini.
Horário: 14:50 – 15:30
Speaker : Hermenegildo Borges de Oliveira – FCT – Universidade do Algarve and CMAFcIO – Universidade de Lisboa – Portugal
Title: Some results on p(u)-Laplacian problems
Abstract: In this seminar, we will approach a new class of nonlinear PDEs problems.
We will study the simple p-Laplacian problem, that gets very complicated when we assume that the exponent of nonlinearity p depends on the solution itself, say u, of the problem.For the associated boundary-value local problem, we prove the existence of weak solutions.We will also emphsize the difficulty of studying this problem from the point of view of Mathematics, especially in knowing in which function space we should look for the solutions.
This is very important to study the uniqueness of solutions, which is a much more difficult task.
Along with the local problem, we shal also consider the non-local variant of this problem.
We will also talk about some results obtained by other authors, departing from our original paper [1], as well as some of the many open problems, and some of the appplications.
The original work underlying this seminar was carried out in collaboration with Michel Chipot from University of Zurich.
References
[1] M. Chipot and H.B. de Oliveira. Some results on the p(u)-Laplacian problem. Mathematische Annalen 375 (2019), 1-2, 283-313.
PROGRAMAÇÃO, QUARTA – FEIRA, 08 DE SETEMBRO
Horário: 14:00 – 14:40
Speaker : Roberto Capistrano-Filho – Dept. of Mathematics , Federal University of Pernanbuco, Brasil
Title: Rapid stabilization of Boussinesq system of KdV-KdV type
Abstract: In this talk we discuss a Gramian-based method introduced by Urquiza in order to stabilize from the boundary a system of two coupled KdV equations. Precisely, we show that it is possible to stabilize this two-equation system by using only one scalar feedback control, being the first time this method is used for a system and improving results already existing in the literature.
Horário: 14:50 – 15:30
Speaker : Jean Silva – Departamento de Matematica, Universidade Federal de Minas Gerais, Brasil
Title: Ergodic functions that are not almost periodic plus L-1 mean zero
Abstract: Ergodic Functions are bounded uniformly continuous (BUC) functions that are typical realizations of continuous stationary ergodic process. It has been a long standing question whether such functions are always the sum of an almost periodic with an L1−mean zero BUC function. In this talk, we answer this question presenting a framework that can provide infinitely many ergodic functions that are not almost periodic plus L1− mean zero.
PROGRAMAÇÃO, QUARTA – FEIRA, 25 DE AGOSTO
Horário: 14:00 – 14:40
Speaker : Viatcheslav Priimenko – State University of Norte Fluminense, National Institute of Science and Technology – Petroleum Geophysics, CNPq – Brazil
Title: Forward and Inverse Problems of Nonlinear Magnetoelasticity
Abstract: The motion of an elastic conductive body in the electromagnetic field is described by the Lamé and Maxwell equations, coupled through so-called nonlinear magnetoelastic effect. In our research we follow the Dunkin-Eringen model due to its simplicity and wide application. First, we consider a mixed initial-boundary value problem. In the 3D-case the main result is the proof of the existence and uniqueness theorem. Uniqueness is proved under additional assumptions on the smoothness of the solution. In the 2D-case we succeeded in proving the uniqueness result without additional a priori
assumptions about the smoothness of the solutions obtained. The situation in a sense is similar to the Navier-Stokes equations. However, unlike the two-dimensional problem for the Navier-Stokes equations, when it was sufficient to use embedding theorems to prove the uniqueness result, we make essential use of the Brézis-Wainger inequality, which allowed to estimate the solution in the L∞-norm and obtain the necessary a priori estimates.
In addition, we prove the solvability of an inverse problem, which consists in identifying the unknown scalar function α(t) in the elastic force α(t)β(x, t) acting on an elastic conductive body when some additional measurement is available.
Horário: 14:50 – 15:30
Speaker : Tomás Caraballo – Dpto. de Ecuaciones Diferenciales y Análisis Numérico, Universidad de Sevilla – Spain
Title: Well-posedness and dynamics of non-local functional partial differential equations
Abstract: In this talk we analyze a non-autonomous nonlocal functional parabolic equation when the external force contains hereditary characteristics involving bounded and unbounded delays. First, well-posedness of the problem is analyzed by the Galerkin method and energy estimations. Moreover, some results related to strong solutions are proved under suitable assumptions. The existence of stationary (steady-state) solutions is then established by a corollary of the Brower fixed point theorem. By constructing appropriate Lyapunov functionals in terms of the characteristic delay terms, a deep analysis on stability and attractiveness of the stationary solutions is established. Eventually, the existence of a non-autonomous (pullback) attractor is considered.
PROGRAMAÇÃO, QUARTA – FEIRA, 11 DE AGOSTO
Horário: 14:00 – 14:40
Speaker : Djairo G. de Figueiredo , IMECC-UNICAMP – Brasil
Title: Pohozaev identity: a hope for existence
Abstract: 1)Pohozaev identity for the Laplacian and general nonlinearities – 2)Pohozaev identity for the p-Laplacian – 3)Some existence results.
Horário: 14:50 – 15:30
Speaker : Diego Souza, Universidad de Sevilla – Spain
Title: Sobre a controlabilidade de algumas EDPs com origem na mecânica dos fluidos
Abstract: As equações de Navier-Stokes suas variantes vem sendo estudadas há muitos anos e sua compreensão é muito relevante do ponto de vista matemático e físico. Muitos pesquisadores têm se preocupado em resolver vários problemas abertos importantes. Por outro lado, o controle dos PDEs tem despertado muita atenção nas últimas décadas. Isso foi motivado por seu papel relevante nas aplicações. Nesta palestra apresentamos alguns resultados recentes tratando com o controle de sistemas do tipo Navier-Stokes.
PROGRAMAÇÃO, QUARTA – FEIRA, 28 DE JULHO
Horário: 14:00 – 14:40
Speaker : Carlos Castro – Universidad Politécnica de Madrid – Spain
Title: Scattering in elastic waves: direct and inverse problem
Abstract: We consider the scattering of waves for the elasticity system with a non-constant matrix potential in dimensions d = 2 and 3.We propose a numerical method to approximate the scattering amplitudes and give some ideas on numerical algorithms to recover the potential from these scatteringdata.
Horário: 14:50 – 15:30
Speaker : André Novotny – Laboratório Nacional de Computação Científica, LNCC / MCTI-Brasil
Title: O Método das Derivadas Topológicas: Teoria e Aplicações
Abstract: A derivada topológica é definida como o primeiro termo da expansão assintótica de um dado funcional de forma com relação ao parâmetro associado ao tamanho de uma perturbação infinitesimal singular – tais como furos, inclusões, termos fonte e até mesmo trincas – introduzida em um ponto arbitrário de um dado domínio geométrico. Ao longo da última década o método das derivadas topológicas tornou-se uma área de pesquisa rica e fascinante, além de bastante ampla dos pontos de vista teórico e numérico, possuindo aplicações em diversos campos de interesse, em especial na otimização de forma e topológica, problemas inversos, processamento de imagens, síntese e/ou projeto ótimo de microestruturas e modelagem de fenômenos dissipativos, incluindo mecânica da fratura e do dano. Esta palestra tem como objetivo introduzir o conceito de derivada topológica e apresentar algumas aplicações nas áreas ora mencionadas. Dessa forma, objetiva-se basicamente mostrar o que é e para que serve a derivada topológica. Sendo assim, a palestra é destinada àqueles interessados nos aspectos matemáticos da análise de sensibilidade topológica, assim como em aplicações do método da derivada topológica na mecânica computacional.
PROGRAMAÇÃO, QUARTA – FEIRA, 14 DE JULHO
Horário: 14:00 – 14:40
Speaker : Jaime Angulo Pava – Department of Mathematics, IME-USP, Brasil
Title: The sine-Gordon equation on metric graphs
Abstract: In this talk we shed new light on the mathematical studies of nonlinear dispersive evolution equations on metric graphs. This trend has been mainly motivated by the demand of reliable mathematical models for different phenomena in branched systems which, in meso- or nano-scales, resemble a thin neighborhood of a graph, such as Josephson junction networks, electric circuits, blood pressure waves in large arteries, or nerve impulses in complex arrays of neurons, just to mention a few examples. Our dynamic problems here will be essentially related to the sine-Gordon model on a Y- junction graph type. Initially, we establish a general linear instability criterium for solitons profiles on arbitrary metric graphs. In the following, we show that some kink or kink/anti-kink soliton profiles for the sine-Gordon model are linearly (and nonlinearly)
unstable.
The arguments presented in this talk have prospects for the study of the instability of soliton-profiles solutions of other nonlinear evolution equations on branched systems.
Horário: 14:50 – 15:30
Speaker : Anna Doubova – Dpto de Ecuaciones Diferenciales y Análisis Numérico, Universidad de Sevilla, Spain
Title: Theoretical and numerical aspects of geometric inverse problems for some PDE’s
Abstract: We will first present the main questions and motivations related to geometric inverse problems for some PDE’s. Then, we will focus our talk on the inverse problems concerning the one-dimensional Burgers equation and some related nonlinear systems (involving heat effects and variable density). In these problems, the goal is to find the size of the spatial interval from some appropriate boundary observations of the solution. Depending on the properties of the initial and boundary data, we prove uniqueness and non-uniqueness results. On the other hand, we also solve these inverse problems numerically and compute approximations of the interval sizes. The presented work has been perfomed in collaboration with Jone Apraiz, Enrique Fernández-Cara and Masahiro Yamamoto.
PROGRAMAÇÃO, QUARTA – FEIRA, 30 DE JUNHO
Horário: 10:00 – 10:40
Speaker : Enrico Valdinoci – University of western – Australia
Title: The Lévy flight foraging hypothesis
Abstract: We consider a forager diffusing via a fractional heat equation and we introduce several efficiency functionals whose optimality is discussed in relation to the Lévy exponent of the evolution equation. Several biological scenarios, such as a target close to the forager, a sparse environment, a target located away from the forager and two targets are specifically taken into account. The optimal strategies of each of these configurations are here analyzed explicitly also with the aid of some special functions of classical flavor and the results are confronted with the existing paradigms of the Lévy foraging hypothesis. Interestingly, one discovers bifurcation phenomena in which a sudden switch occurs between an optimal (but somehow unreliable) Lévy foraging pattern of inverse square law type and a less ideal (but somehow more secure) classical Brownian motion strategy. Additionally, optimal foraging strategies can be detected in the vicinity of the Brownian one even in cases in which the Brownian one is pessimizing an efficiency functional.
Horário: 10:50 – 11:30
Speaker : Anderson Ramos – Universidade Federal do Pará – Brazil
Title: Stability conditions of Timoshenko system with thermodiffusion effects and second sound
Abstract: In this presentation we consider a new Timoshenko beam model with thermal and mass diffusion effects where heat and mass diffusion flux are governed by Cattaneo’s law. Necessary and sufficient conditions for exponential stability are provided in terms of the physical parameters of the model. Firstly, by the C_0−semigroup theory, we prove the well-posedness of the considered problem. Then we prove the lack of exponential stability of the system when one of these conditions is not valid. Finally, we prove in this case that the semigroup decays to zero polynomially as 1/t^{1/2}. Moreover we show that the rate is optimal.
PROGRAMAÇÃO, QUARTA – FEIRA, 16 DE JUNHO
Horário: 14:00 – 14:40
Speaker : Hermano Frid – Instituto de Matemática Pura e Aplicada (IMPA-Brasil)
Title: Short wave-long wave interactions for conservation laws in the relativistic context.
Abstract: In this talk we introduce a framework for modeling the short wave-long wave interactions in the relativistic context. In this context the nonlinear Schr\”odinger equation is no longer suitable for describing short waves and is replaced by a Klein-Gordon equation. Two specific examples are considered: the case where the long waves are governed by a relativistic Burgers equation; and the case where the long waves are governed by the augmented Born-Infeld equations in electromagnetism. This is a joint work with João Paulo Dias.
Horário: 14:50 – 15:30
Speaker : Valéria Cavalcanti – Universidade Estadual de Maringá (UEM-Brasil)
Title: Global existence and asymptotic behaviour of weak solutions for the viscoelastic wave equation with supercritical source
Abstract: The modern viscoelasticity has its origin in the works of Boltzmann and Volterra, who made a connection between the notion of memory with elastic materials. In this talk we are concerned with the uniform decay of the energy as well as the blow-up of weak solutions for the viscoelastic wave equation with localized memory with past history and supercritical source terms. This is a joint work with M. M. Cavalcanti, T. D. Marchiori and C. M. Weber.
PROGRAMAÇÃO, QUARTA – FEIRA, 02 DE JUNHO
Horário: 14:00 – 14:40
Speaker : Ma To Fu, Department of Mathematics, University of Brasília, Brasil.
Title: Attractors for a semilinear elasticity system featuring damping-vs-delay
Abstract: In this talk we discuss the long-time dynamics of weakly dissipative elasticity systems with delay effects on the velocity. This damping-vs-delay feature was firstly considered by Nicaise and Pignott (2006) in the context of interior and boundary controllability for wave equations. Our objective is to establish the existence of a smooth finite dimensional global attractor, allowing nonlinearities of critical growth. The main difficulty is finding necessary arguments to show that the system is quasi-stable in the sense of Chueshov and Lasiecka.
References:
[1] S. Nicaise and C. Pignotti, Stability and instability results of the wave equation with a delay term in the boundary or internal feedbacks, SIAM J. Control Optim. 45 (2006) 1561-1585.
[2] I. Chueshov and I. Lasiecka, Von Karman Evolution Equations. Well-Posedness and Long-Time Dynamics, Springer Monographs in Mathematics, Springer, New York, 2010.
[3] T. F. Ma, J. G. Mesquita and P. N. Seminario-Huertas, Smooth dynamics of weakly damped Lamé systems with delay, SIAM J. Math. Anal. (to appear).
Horário: 14:50 – 15:30
Speaker : Fernanda Cipriano Department of Mathematics, Universidade NOVA de Lisboa, Portugal
Title: Optimal portfolio for the α-Hypergeometric stochastic volatility model
Abstract: In this talk we study an optimal portfolio problem for an investor with constant relative risk aversion that trades in a market with asset prices described by the α-Hypergeometric stochastic volatility model introduced by Fonseca and Martini.To determine the optimal strategy, we follow the dynamic programming approach. Namely, using a suitable Feynman-Kac representation, we construct a classical solution for the corresponding Hamilton-Jacobi-Bellman equation. In order to verify that the solution of the Hamilton-Jacobi-Bellman equation coincides with value function, we establish a verification theorem.
In addition, we present numerical simulations for the approximation of the value function using a method based on the proposed Feynman-Kac representation.This is a joint work with Nuno Martins and Diogo Pereira.
PROGRAMAÇÃO QUARTA – FEIRA, 19 DE MAIO
Horário: 14:00 – 14:40
Speaker : Nicolas Burq , Université Paris-Sud, France
Title: Decay rates for Kelvin Voigt damped wave equations
Abstract: In this talk I will present some recent results about the decay of wave equations with visco-elastic dampings. I will in particular highlight the convergences and differences between this kind of damping and the more classical ones, in terms of — Propagation of singularities — Overdamping phenomena “too much damping kills the damping” — Boundary value problems analysis This is based on joint works with Chenmin Sun (University of Cergy-Pontoise)
Horário: 14:50 – 15:30
Speaker : Maria Soledad Aronna , Escola de Matemática Aplicada (FGV EMAp), Brasil
Title: Modeling and analysis of Sterile Insect Technique (SIT) implementation strategies for vector and pest control
Abstract: Joint work with Yves Dumont (CIRAD, Reunion Island, France; and AMAP, University of Montpellier, CIRAD, France; and Department of Mathematics and Applied Mathematics, University of Pretoria,Pretoria, South Africa).
The Sterile Insect Technique (SIT) is a biological control method that consists of releasing males that have been sterilized using ionizing radiation. In the wild, these males mate with wild females that will not produce viable offsprings.
In this talk we present a minimalist model for SIT, assuming that residual fertility can occur in the sterile male population after radiation. Taking into account that we are able to get regular measurements from the biological system along the control duration, such as the size of the wild insect population, we investigate different release strategies that involve either continuous or periodic impulsive releases, in open- and closed-loop forms. We show that a combination of open-loop control with constant large releases and closed-loop nonlinear control leads to the best strategy in terms of both number of releases and total quantity of sterile males to be released. Additionally, we show that SIT fails if the residual fertility is greater than a threshold value that depends on the wild population biological parameters. Moreover, even for small values, the residual fertility induces the use of such large releases, that SIT alone is not always reasonable from a practical point of view.
We provide applications against the mosquito species Aedes albopictus and the fruit fly Bactrocera dorsalis.
PROGRAMAÇÃO QUARTA – FEIRA, 05 DE MAIO
Horário: 14:00 – 14:40
Speaker : Jean Pierre Puel , Université de Versailles Saint-Quentin France
Title: Localisation of energy and localised controllability
Abstract: We consider the wave equation or the Schr\ödinger equation on a domain \Omega. We can define the localised energy on a subdomain D and the starting point of this work was to find an action (control) on the equation in order to obtain a prescribed value of this localised energy. It turns out that this question is equivalent to a localised controllability problem (in the subdomain D). We shall give answers to these questions under some conditions and also some open problems.
Horário: 14:50 – 15:30
Speaker : Amaury Alvarez Cruz , Instituto de Computação UFRJ – Brazil
Title: Transformation to structured perturbations usingexplicit recurrent procedure for a given family of matrix pencils
Abstract: Matrix polynomials arise in several applications in optimal control, engineering and linear systems theory. One of the practical uses is as approximations of highly nonlinear eigenvalue problems. In this work, we find verssal deformation of Fiedler linearization of the perturbation of matrix coefficients of a polynomial. We focus on the first companion form but the method presented here is possible to extend to a broader class of linearizations. We applied the explicit recurrent procedure to construct a smooth deformation. This construction serves to characterize the perturbation of matrix polynomials and its linearization. Other applications studying the resonance phenomena in the system of conservation laws are presented.
PROGRAMAÇÃO QUARTA – FEIRA, 20 DE ABRIL
Horário: 14:00 – 14:40
Speaker : Manuel Milla Miranda , Universidade estadual de paraiba UEPB-Brasil
Title: Longitudinal Vibrations of a Bar
Abstract: This conference is concerned with the results on the equation of the small longitudinal vibration of a bar whose one end is clamped and the other end is glued to a concentrated mass.
Horário: 14:50 – 15:30
Speaker : Saulo Pomponet Oliveira , Universidade Federal Do Parana UFPR-Brasil
Title: Métodos aerogeofísicos
Abstract: A interação entre computação científica e geofísica de exploração ocorre predominantemente nos métodos sísmicos, que trazem desafios notáveis na solução de problemas diretos e inversos de propagação de ondas. Talvez
menos conhecidos fora dos departamentos de geologia e de geofísica, métodos aerogeofísicos como a aeromagnetometria e a aerogamaespectrometria também fomentam a pesquisa em técnicas numéricas. O estudo destes métodos é interessante pela disponibilidade de dados obtidos pelo Serviço Geológico do Brasil (CPRM) em levantamentos aéreos que cobrem vasta área do território nacional. Esta apresentação traz um panorama da matemática computacional envolvida, que inclui métodos iterativos de inversão como na sísmica, porém há uma demanda maior por técnicas voltadas para problemas estacionários em vez de transientes.
PROGRAMAÇÃO QUARTA – FEIRA, 07 DE ABRIL
Horário: 14:00 – 14:40
Speaker : Harald Helfgott , Universität Göttingen- Alemanha y CNRS-Francia
Title: Los grafos expansores y el problema de paridad.
Abstract: La noción de grafo expansor puede definirse de varias maneras equivalentes: en términos de las fronteras de conjuntos de vértices, o de valores propios del Laplaciano, o de caminatas aleatorias… Los grafos expansores se han convertido en un objeto central de estudio en las matemáticas discretas; aparte de sus variadas aplicaciones en el estudio de algoritmos, aparecen en la teoría de grupos, la combinatoria y también en la teoría de números. Aparte de dar una introducción a los grafos expansores, hablaré de un resultado reciente mío (todavía por aparecer!) conjunto con M. Radziwiłł. Probamos que unos grafos que codifican cuáles primos en un rango dividen a cada entero son grafos expansores, en un sentido por cierto fuerte. En tanto que corolarios (y usando también un resultado de Matomäki-Radziwiłł-Tao), obtenemos que
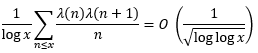
lo cual mejora el resultado de Tao sobre la conjectura de Chowla logarítmica en grado 2. Obtenemos también una mejora sobre el trabajo de Tao-Teräväinen sobre la conjectura de Chowla a casi toda escala.
Horário: 14:50 – 15:30
Speaker : Edgard Pimentel , Pontifícia Universidade Católica do Rio de Janeiro -Brasil
Title: Fully nonlinear free transmission problems
Abstract: We consider a discontinuous fully nonlinear elliptic operator whose discontinuities depend on the solutions. Such dependence frames the model in the context of free boundary problems. We discuss the optimal regularity of strong solutions and study the free boundary. In addition, under fairly natural conditions, we prove the existence of $L^p$-viscosity solutions and the existence of strong solutions to the Dirichlet problem associated with our model. This is based on joint works with Makson Santos (CIMAT, Mexico) and Andrzej Święch.
PROGRAMAÇÃO QUARTA – FEIRA, 24 DE MARÇO
Horário: 14:00 – 14:40
Speaker : Irena Lasiecka – University of Memphis Department of Mathematical Sciences-United States of America
Title: JMGT [Jordan-Moore Gibson-Thompson] dynamics arising in nonlinear acoustics – a view from the boundary.
Abstract: A third-order (in time) JMGT equation is a nonlinear (quasilinear) Partial Differential Equation (PDE) model introduced to describe a nonlinear propagation of high frequency acoustic waves. The interest in studying this type of problems is motivated by a large array of applications arising in engineering and medical sciences-including high intensity focused ultrasound [HIFU] technologies, lithotripsy, welding and others. The important feature is that the model avoids the infinite speed of propagation paradox associated with a classical second order in time equation referred to as Westervelt equation. Replacing a classical heat transfer by heat waves gives rise to the third order in time derivative scaled by a small parameter τ > 0, the latter represents the thermal relaxation time parameter and is intrinsic to the properties of the
medium where the dynamics occurs.
The aim of the present lecture is to provide a brief overview of recent results in the area which are pertinent to both linear and non-linear dynamics. From the mathematical point of view JMGT, can be seen as a nonlinear perturbation of a third order strictly hyperbolic system, which however has a characteristic boundary. This feature has, of course, strong implications on boundary behavior [both regularity and controllability] which can not be patterned after classical hyperbolic systems theory [as it is the case for the wave equation]. As a consequence, the analysis of regularity [both forward and inverse estimates] is
particularly challenging-even in the linear case. Several recent results pertaining to boundary stabilization, with Neumann non-dissipative boundary and related optimal control with boundary actuation and infinite horizon will be presented
and discussed. In all these case, peculiar features associated with the third order dynamics leads to novel phenomenological behaviors. The work presented is in collaboration with Marcelo Bongarti and Jose Rodriguez.
Horário: 14:50 – 15:30
Speaker : Jaqueline Godoy Mesquita – Universidade de Brasília, UnB – Brasil
Title: Linearized instability for neutral functional differential equations with state-dependent delays.
Abstract: In this talk, we will give a brief overview of a class of equations called _neutral functional differential equations with state-dependent delays_, describing some important applications. After this, we will show some recents results in the area, and we will present a principle of linearized instability for these equations.This is a joint work with Professor Bernhard Lani-Wayda
PROGRAMAÇÃO QUARTA – FEIRA, 10 DE MARÇO
Horário: 14:00 – 14:40
Speaker : Marcelo Moreira Cavalcanti – Universidade Estadual de Maringá – Brasil
Title: Exponential decay for the semilinear wave equation with localized frictional and Kelvin-Voigt dissipating mechanisms
Abstract: In the present talk, we are concerned with the semilinear viscoelastic wave equation in an inhomogeneous medium $\Omega$ subject to two localized dampings. The first one is of the type viscoelastic and is distributed around a neighborhood $\omega$ of the boundary according to the Geometric Control Condition. The second one is a frictional damping and we consider it hurting the geometric condition of control. We show that the energy of the wave equationgoes uniformly and exponentially to zero for all initial data of finite energy taken in bounded sets of finite energy phase-space.
Horário: 14:50 – 15:30
Speaker : Eduardo González – Pontificia Universidad Catolica de Valparaiso-Chile
Title: Bifurcaciones, periodicidad y multiples estabilidades en modelos de depredacion de tipo Gause. Una breve revision
Abstract: En esta presentacion expondremos las principales propiedades de un tipo de modelos compartimentados de depredacion tiempo continuo, denominados modelos de tipo Gause [2]. Es bien sabido que las interacciones depredador-presa dependen fuertemente tanto de las tasas de crecimiento de la poblacion de presas y depredadores, como
de la acciÛn de depredaciÛn denominada la respuesta funcional [7]. Esta funcion la consideraremos solo dependiente de la poblacion de presas (respuesta funcional presa-dependiente) [6], usando principalmente las formas matematicas mas usuales [3], clasificadas como tipos Holling I, II, III y IV [4]. El objetivo principal será establecer condiciones para la existencia o no de ciclos lÌmites (soluciones periodicas) [1] y algunas de las bifurcaciones mas conocidas en sistemas planares tiempo continuo [5].
[1] K.S.Cheng, Uniqueness of a limit cycle for a predator-prey system, SIAM Journal on Applied Mathematics 12 (1981) 541-548.[2] G. F. Gause, The struggle for existence, The Williams & Wilkins company, 1934. [3] E. Gonz·lez-Olivares and A. Rojas-Palma, Allee e§ect in Gause type predator-prey models: Existence of multiple attractors, limit cycles and separatrix curves. A brief review. Mathematical Modelling of Natural Phenomena 8(6) (2013) 143-164. [4] C. S. Holling, The components of predation as revealed by a study of small-mammal predation of the European pine sawáy, Canadian Entomologist 91(1959) 293-320. [5] Y. A. Kuznetsov, Elements of applied bifurcation theory (2nd Edition), Springer-Verlag (1998). [6] R. M. May, Stability and complexity in model ecosystems (2nd edition), Princeton University Press (2001). [7] P. Turchin, Complex Population Dynamics: A Theoretical/Empirical Synthesis, Princeton University Press, Princeton, New Jersey, 2003.
PROGRAMAÇÃO QUARTA – FEIRA, 24 DE FEVEREIRO
Horário: 14:00 – 14:40
Speaker : Sérgio Almaraz – Universidade Federal Fluminense -UFF, Brasil
Title: Teoremas de massa positiva e problemas do tipo Yamabe
Abstract: O problema de Yamabe é uma questão de uniformização de variedades Riemannianas que foi proposta em 1960. Essa questão proporcionou enorme desenvolvimento no emprego de técnicas de Equações Diferenciais Parciais em Geometria Diferencial. O passo final na sua resolução, dado por R. Schoen em 1984, apresentou uma relação entre o problema de Yamabe e a teoria da Relatividade Geral de Einstein. Esse passo envolve a prova do teorema da massa positiva para sistemas isolados assintoticamente planos. Nessa palestra, discutirei um pouco os conceitos básicos envolvidos no tema bem como problemas similares e recentes, apresentando um pouco das minhas linhas de pesquisa e resultados relacionados
Horário: 14:50 – 15:30
Speaker : Roxana Lopez Cruz – IDIC-ULIMA Y UNMSM, Perú
Title: Un modelo epidemiológico SAIRD con retroalimentación negativa
Abstract: Las epidemias por su naturaleza dinámica tienen su modelación matemática básica la cual se va tornando más compleja según como se vaya considerando más factores que caracterizan a cada enfermedad. Sin embargo, hay factores externos a la enfermedad que influencian en la incidencia de esta y ellos son generados por ejemplo por prejuicios sobre campañas de vacunación con previa información (retroalimentación negativa), como el caso del concepto negativo en la población con respecto a la vacuna contra el virus del papiloma humano (VPH), muchas veces causado por desinformación. En este trabajo proponemos y analizamos un modelo epidémico en ecuaciones diferenciales que define la función índice de información y el efecto de la retroalimentación negativa en el parámetro de tratamiento no farmacéutico (por ejemplo: cuarentenas). Los resultados matemáticos y de simulación nos proporcionaran los diversos escenarios de la dinámica de la enfermedad que nos ayudara a mostrar la importancia por ejemplo de una buena información en cuanto a las cuarentenas.
PROGRAMAÇÃO QUARTA – FEIRA, 10 DE FEVEREIRO
Horário: 14:00 – 14:40
Speaker : Alexandre Madureira, Laboratorio Nacional de Computaçao Cientifica-LNCC-Brasil
Title: Multi-generational SIR modeling: determination of parameters, epidemiological forecasting and age-dependent vaccination policies
Abstract: We use an age-dependent SIR system of equations to model the evolution of the COVID-19. Parameters that measure the amount of interaction in different locations (home, work, school, other) are approximated using a random optimization scheme, and indicate changes in social distancing along the course of the pandemic. That allows the estimation of the time evolution of the classical and age-dependent reproduction numbers $\R_0$. With those parameters we predict the disease dynamics, and compare our results with data from several locations in Brazil. We also provide a preliminary investigation regarding age-based vaccination policies, indicating connections between the age of those immunized, contagious parameters and vaccination schedules.
Horário: 14:50 – 15:30
Speaker :Mauricio Sepúlveda Cortés, Departamento de Ingenieria Matemática, Universidad de Concepción-Chile
Title: Energy Conservative Finite Difference Methods for Dispersive Equations
Abstract: Some numerical methods are presented for equations that model the propagation of waves or dispersive solitons, such as the Korteveg-de Vries as fluid models, or the high-order Schrödinger equation with applications in wave propagation in optical fibers. In these models the nonlinear terms generate some difficulties both in the analysis and in the numerical approximations. Within the possibilities, a numerical discretization is chosen that conserves the L2 norm or the energy associated with the equation. This helps to make discrete estimates of energy and demonstrate stability. Additionally, the stability and exponential decay of energy is studied by adding different types of damping or memory terms on the equations
PROGRAMAÇÃO QUARTA – FEIRA, 27 DE JANEIRO
Horário: 14:00 – 14:40
Speaker : André Nachbin, Instituto de Matemática Pura e Aplicada-IMPA, Brasil
Title: Integração singular visando um operador de diferenças finitas com precisão espectral
Abstract: É sabido que um operador de diferenças finitas aproxima uma derivada apresentando uma taxa (fixa) de convergência algébrica. No entanto, vamos exibir um novo operador de diferenças finitas e provar que tem precisão espectral. Ou seja, a taxa de convergência não é fixa e melhora de acordo com a regularidade da função. Por exemplo, a convergência é exponencial para funções analíticas. Nossa metodologia não é padrão em Teoria da Aproximação, pois não usa aproximação polinomial nem qualquer outro tipo de base. Nosso método se baseia simplesmente na manipulação numérica de integrais singulares, usando quadraturas precisas para integrais do tipo Valor Principal de Cauchy. O núcleo da integral é uma distribuição, o que dá lugar a um esquema multi-resolução. O respectivo método de diferenças finitas distribucional apresenta “stencils” de todas as resoluções possíveis na grade, estimando derivadas de uma forma não-local. Apresentaremos ilustrações computacionais deste novo método e faremos comparações com outro método recente (não-convencional) de diferenças finitas, que faz uso de um passo complexo para lidar melhor com o erro de arredondamento.
Horário: 14:50 – 15:30
Speaker :Eduardo Cerpa, Instituto de Ingeniería Matemática y Computacional- Pontificia Universidad Católica de Chile, Chile
Title: Effect of time scales on stability of coupled systems involving the wave equation
Abstract: This talk considers systems coupling an ordinary differential equation (ODE) with a wave equation through its boundary data. The main focus is put on the role of different time scales for each equation on the stability of the coupled system. In this context it is natural to apply the singular perturbation method but for infinite-dimensional systems it is known that in some cases this method does not work. Indeed, you can not be sure of the stability of the full system even if the given subsystems are stable. This is the case when coupling a wave equation to a fast ODE. On the other hand, when coupling a fast wave equation with an ODE, the system is proven to be stable if each subsystem is stable. We use the singular perturbation method to get that result and a Tikhonov theorem, which is the first of this kind for systems involving the wave equation.
PROGRAMAÇÃO QUARTA – FEIRA, 13 DE JANEIRO
Horário: 14:00 – 14:40
Speaker : Octavio Paulo Vera Villagran
Title: Exact Solution For a Benney-Lin Equation Type
Abstract: An exponential traveling-wave solution of the free surface equation for a viscous film flowing down an inclined plane is presented. We use the Ince transformation.
Horário: 14:50 – 15:30
Speaker : Teófilo Domingos Chihaluca, Universidade da Beira Interior
Title: Aproximação Numérica de Equações Diferenciais Parciais Não Lineares com Aplicação em Finanças
Abstract: É feita a regularização da equação Delta de Black-Scholes não linear para o modelo de custo de transação. Prova-se a existência de solução clássica da equação regularizada e prova-se que esta converge para a solução viscosa do problema. Demonstra-se que a ordem convergência da solução semi-discreta e a da totalmente discreta. Para o cálculo de opções americanas, acrescentou-se um termo de penalidade no segundo membro e a condição da derivada para localizar a fronteira. No final, o método é implementado em ambiente Matlab e são apresentados alguns resultados numéricos.
PROGRAMAÇÃO, QUARTA – FEIRA, 16 DE DEZEMBRO
Horário: 14:00 – 14:40
Speaker : Diogo Gomes , King Abdullah University of Science and Technology-Saudi Arabia
Title: Algorithms for PDEs
Abstract: The qualitative study of PDEs often relies on integral identities and inequalities. For example, for time-dependent PDEs, conserved integral quantities or quantities that are dissipated play an important role. In particular, if these integral quantities have a definite sign, they are of great interestas they may provide control on the solutions to establish well-posedness. Finding these integral identities and inequalities is a tedious task that relies on a combination of heuristics and skill. However, as we will see in this talk, finding conserved and dissipated quantities for PDEs is an algorithmic task that can be automated. We will discuss some ongoing progress in this area,the key tools used (exact linear algebra, calculus of variations and quantifier elimination methods) and present some applications to the theory of mean-field games. We will also address semi-discretization of partial differential equations and how our methods can be used in these problems.
Horário:14:50 – 15:30
Speaker : Sandra Malta , Laboratório Nacional De Computação Cientifica-Brazil
Title: Um modelo SEIRD generalizado para a COVID-19 com mecanismo implícito de distanciamento social.
Abstract: Desenvolvemos um modelo SEIRD generalizado onde são consideradas medidas de distanciamento social, com o objetivo de deter a disseminação da COVID-19. Para a identificação dos parâmetros dos modelos e a quantificação das incertezas é aplicada uma análise bayesiana. Diferentes estratégias de relaxamento das medidas de distanciamento social são investigadas, buscando aquelas que produzem maior impacto no achatamento da curva de infectados. São apresentados resultados para o Brasil e o estado do Rio de Janeiro.
PROGRAMAÇÃO, QUARTA – FEIRA, 02 DE DEZEMBRO
Horário: 14:00 – 14:40
Speaker : Luz de Teresa, Universidade Federal de Paraíba/ Universidad Nacional Autónoma de México
Title: Algunos resultados de diseño de observadores para EDP
Abstract: El problema del diseño de observadores surge de la necesidad de monitorear sistemas de control en tiempo real. Es decir, se busca estimar, de la mejor manera, las variables de estado del sistema, a partir de la informaci on (limitada) medible obtenida del sistema. Dicha informaci on es obtenida mediante sensores colocados en regiones accesibles del sistema, ya sea en el interior o en la frontera del dominio del sistema. El diseño de observadores tiene diversas aplicaciones, por ejemplo en detecci on de fallas, estimaci on de par ametros, reconstrucci on de modelos. En esta charla presentaremos algunos resultados para la ecuación del calor semilineal y presentaremos algunos avances para la ecuación de ondas.
Horário:14:50 – 15:30
Speaker : Antônio Leitão, Universidade Federal de Santa Catarina , Brazil
Title: Uma tarde com problemas inversos e mal-postos
Abstract: Nesta palestra será apresentada, por meio de exemplos, uma área de pesquisa da matemática aplicada, a saber “problemas inversos”. Algumas questões desafiadoras relacionadas aos problemas matemáticos dessa área serão o discutidas. A tarefa de como obter soluções (de forma estável) para problemas mal-postos será investigada.
PROGRAMAÇÃO, QUARTA – FEIRA, 18 DE NOVEMBRO
Horário: 14:00-14:40
Speaker: Felipe Linares, Instituto de Matemática Pura e Aplicada (IMPA) Brazil
Title: On long time behavior of solutions of the Schrödinger-Korteweg-de Vries system
Abstract: In this lecture we will be concerned with the decay of long time solutions of the initial value problem associated with the Schrödinger-Korteweg-de Vries system. We use recent techniques in order to show that solutions of this system decay to zero in the energy space. Our result is independent of the integrability of the equations involved and it does not require any size assumptions.
Horário: 14:50-15:30
Speaker: Paulo Amorim, Instituto de Matemática da Universidade Federal de Rio de Janeiro (IM-UFRJ) Brazil
Title: A model of self-propelled agents interacting through pheromone: individual and collective behavior
Abstract: We present a model of self-propelled agents navigating on a landscape oriented by a pheromone signal. The model is heavily motivated by ant navigation. We begin by deducing the model from biological considerations, where each individual orients itself according to the presence of the pheromone in a small circular sector around it. We present some stability properties of trail-like solutions when the trail is given, showing that trail-following behavior is a stable feature of the model. Next, we show the model’s consistency with some experimental results. We proceed to the analysis of the model in the case where the pheromone field is produced by a large number of interacting agents. This gives rise to a system of $N$ ODEs coupled by a diffusion equation, which we analyze. Finally, we provide some numerics to illustrate the collective, self-organizing behavior.
PROGRAMAÇÃO, QUARTA – FEIRA, 04 DE NOVEMBRO
Horário: 14:00-14:40
Palestrante: Marko Rojas-MedarUniversidad de TarapacáArica, Chile
Titulo: Formalismo de Duvobitski-Milyutin e suas aplicações em EDP
Resumo: Apresentamos uma revisão da teoria desenvolvida por Dubovitskii e Milyutin sobre as condições de otimalidade para problemas de otimização com um ou múltiplos objetivos. Os resultados de Dubovitskii e Milyutin permitem obter condições de otimalidade para problemas de otimização em espaços localmente convexos e podem ser aplicados em diferentes áreas. Em particular, mostraremos sua aplicação na caracterização do ótimo no sentido de Pareto e Nash quando a dinâmica do sistema é governada pelas equações de Navier-Stokes.
Horário: 14:50-15:30
Speaker: Sônia M. Gomes – IMECC-Unicamp Brazil
Title: Two-scale Hybrid-Mixed Methods for Linear Elasticity with Weak Stress Symmetry
Abstract: We present a multiscale hybrid-mixed method for linear elasticity problems on general polytope meshes. The new methods approximate displacement, stress, and rotation using two-scale discretizations. The first scale level setting consists of approximating the traction variable (Lagrange multiplier) in discontinuous polynomial spaces, and of computing rigid body modes element wisely. In the second level, the methods are made effective by solving completely independent local boundary Neumann elasticity problems written in a mixed form with weak symmetry enforced via a rotation multiplier. Since the finite-dimensional space for the traction variable constraints the local stress approximations, the discrete stress field lies in the H(div) space globally and stays in local equilibrium with external forces. We propose different choices to approximate local problems based on pairs of finite element spaces defined on affine second-level meshes. Those choices generate the family of multiscale finite element methods for which stability and convergence are proved in a unified framework. Notably, we prove that the methods are optimal and highorder convergent in the natural norms. Also, it emerges that the approximate displacement and stress divergence are super-convergent in the L2-norm. Numerical verifications assess theoretical results and highlight the high precision of the new methods on coarse meshes for multilayered heterogeneous material problems. Joint work with: P. R. Devloo, A. M. Farias, A. B. dos Santos, W. Pereira and F. Valentin
PROGRAMAÇÃO, QUARTA – FEIRA, 21 DE OUTUBRO
Horário: 14:00-14:40
Speaker: Boyan Sirakov , Departamento de MatemáticaPUC – Rio, Brasil
Title: A LIOUVILLE-TYPE THEOREM FOR THE LANE-EMDEN EQUATION IN A HALF-SPACE
Abstract: We prove that the Dirichlet problem for the Lane-Emden equation in a halfspac has no positive solution which is monotone in the normal direction. As a consequence, this problem does not admit any positive classical solution which is bounded on finite strips. This question has a long history and our result solves a long-standing open problem. Such a nonexistence result was previously available only for bounded solutions, or under a restriction on the power in the nonlinearity. The result extends to general convex nonlinearities.
Horário: 14:50-15:30
Speaker: Francisco Manuel Guillen Gonzalez, Dpto. de Ecuaciones Diferenciales y Análisis Numérico Universidad Sevilla, Spain
Title: Some bilinear optimal control problems related to chemotaxis PDE models
Abstract: In this talk we show some recent results for bilinear optimal control subject to several chemo-repulsion and production models (changing the production function). Three type of results will be presented; existence of global optimal solution, a necessary optimality system based on the existence of Lagrange multipliers, and a posteriori regularity result for these Lagrange multipliers.
PROGRAMAÇÃO, QUARTA – FEIRA, 07 DE OUTUBRO
Horário: 14:00-14:40
Speaker: Jorge P Zubelli , Khalifa University, Abu Dhabi, UAE , IMPA, Rio de Janeiro, Brazil
Title: A Splitting Strategy for the Calibration of Jump-Diffusion Models
Abstrac: This talk concerns the calibration of Dupire’s model in the presence of jumps. This leads to an integro-differential equation whose parameters have to be calibrated so as to fit market data. We present a detailed analysis and implementation of a splitting strategy to identify simultaneously the local-volatility surface and the jump-size distribution from quoted European prices. The underlying model consists of a jump-diffusion driven asset with time and price dependent volatility.
Our approach uses a forward Dupire-type partial-integro-differential equation for the option prices to produce a parameter-to-solution map. The ill-posed inverse problem for such a map is then solved by means of a Tikhonov-type convex regularization. We present numerical examples that substantiate the robustness of the method both for synthetic and real data. This is joint work with Vinicius Albani (UFSC) that just appeared in Finance and Stochastics.
Horário: 14:50-15:30
Palestrante: Maicon R. Correa , Instituto de Matemática, Estatística e Computação Científica, Unicamp – Brazil
Titulo: Numerical Schemes for Multiphase Flow in Poroelastic Media
Resumo: In this talk, we present a sequential iterative algorithm for numerically solving the coupled nonlinear system of partial differential equations that models multiphase-flow in highly heterogenous poroelastic media, and discuss the use of different mixed Finite Element Methods for the (linearized) elliptic subproblems of flow and geomechanics. In particular, we focus on the use of accurate and stable mixed-hybrid finite element methods to compute Darcy’s velocity and pressure in highly heterogeneous porous media and the pair stress-displacement in linearly elastic isotropic media.
PROGRAMAÇÃO, QUARTA – FEIRA, 23 DE SETEMBRO
Horário: 14:00 – 14:40
Conferencista: Enrique Zuazua
Friedrich-Alexander-Universität Erlangen-Nürnberg, Germany
Deusto Foundation, Bilbao, Spain
Universidad Autónoma de Madrid, Spain
Título: Control Turnpike y Aprendizaje Profundo
Resumo: El principio de Turnpike afirma que en grandes horizontes temporales las estrategias de control óptimas son casi de naturaleza estacionaria. En esta conferencia estudiaremos algunos resultados recientes sobre este tema y presentaremos algunas de sus consecuencias en el aprendizaje supervisado profundo. La charla se basará en particular en el reciente trabajo conjunto con C. Esteve, B. Geshkovski y D. Pighin.
Horário: 14:50 – 15:30
Palestrante: Daniel G. Alfaro Vigo (Departamento de CIência da Computação – UFRJ)
Título: Um método aproximado para a equação de Korteweg-de Vries com dissipação
Resumo: A equação de Korteweg-de Vries (KdV) representa um modelo matemático simplificado da propagação, em um meio dispersivo, de ondas unidirecionais não lineares e de pequena amplitude. Nos últimos anos a equação KdV com dissipação tem despertado muito interesse na comunidade matemática. Nesta palestra, vamos apresentar resultados sobre a existência e unicidade de soluções, e a influência do mecanismo de dissipação na energia do sistema para a equação KdV com dissipação em um domínio limitado. Será abordado um método numérico baseado na discretização por elementos finitos no espaço e pelo esquema de diferenças finitas de Crank-Nicolson no tempo. Será apresentada a análise numérica desse método aproximado e também discutiremos os resultados de simulações numéricas. Este trabalho foi realizado em colaboração com Mauro A. Rincon (UFRJ) e Juliana C. Xavier (UTFPR).
PROGRAMAÇÃO, QUARTA – FEIRA, 09 DE SETEMBRO
Horário: 14:00 – 14:40
Speaker: E. Fernández-Cara, Universidad de Sevilla (Spain)
Title: Controlling fluids: motivations and some recent results
Abstract: The Navier-Stokes equations have been studied since many years. They are very relevant in mathematics and physics and many people have been concerned with the solution of several related major open problems. On the other hand, the control of PDEs has attracted a lot of work the last decades. This has been motivated by its relevant role in applications. This talk is devoted to present some recent results dealing with the control of systems of the Navier-Stokes kind. We will consider some (new) optimal control and controllability problems and we will discuss theoretical and numerical aspects.
Horário: 14:50 – 15:30
Palestrante: Nuno Crokidakis, Instituto de Física, Universidade Federal Fluminense (Brasil)
Título: Analisando o potencial para uma segunda onda de casos na evolução da COVID-19 em economias emergentes e em desenvolvimento
Resumo: O distanciamento social, alcançado pela restrição da mobilidade humana, é apontado como a estratégia mais eficiente contra a evolução da COVID-19. No entanto, pressões econômicas dificultam a implementação dessa medida. Em primeiro lugar, os indivíduos que dependem dos rendimentos da economia informal são mais afetados por tais restrições e, consequentemente, menos propensos a respeitar as políticas de restrição à mobilidade. Em segundo lugar, se as restrições forem suspensas logo após os níveis de infecção atingirem um pico e começarem a diminuir continuamente, uma segunda onda de infecções pode surgir e aumentar o custo da pandemia. Analisamos o impacto desses dois fatores na evolução da pandemia de COVID-19 através de um modelo de duas populações Suscetível-Infectado-Recuperado-Assintomático-Sintomático-Morto (SIRASD), onde os indivíduos diferem apenas pelo seu grau de conformidade com políticas de distanciamento social. Embora nossa abordagem seja válida para qualquer país emergente, onde o número de pessoas envolvidas na economia informal representa uma grande parcela da força de trabalho total e, portanto, propenso a não seguir o auto-isolamento, usamos dados do Brasil, um país que apresenta estas características, a fim de fornecer resultados numéricos convincentes. Com base em parâmetros derivados de dados de propagação da COVID-19 no Brasil, concluímos que se as medidas de confinamento forem suspensas muito cedo, ou seja, até uma semana de diminuição consecutiva do número de novos casos, é muito provável que o aparecimento de um segundo pico.
PROGRAMAÇÃO, QUARTA-FEIRA, 26 DE AGOSTO
14:00 – 14:40
Speaker: Roberto Guglielmi, Department of Applied Mathematics, University of Waterloo, Canadá
Title: Bilinear Optimal Control of the Fokker-Planck Equation
Abstract: For a large class of stochastic processes, the evolution of the probability density function associated to the process is ruled by the Fokker-Planck equation. Following a statistical approach, we recast an optimal control problem subject to a stochastic differential equation in terms of an optimal control problem for the Fokker-Planck equation. Motivated by this relation, in this talk we study the optimal control problem of the Fokker-Planck equation through a bilinear control acting as the coefficient of the divergence in the advection term. We extend previous results to the case of a control which depends on time and space. We give suitable conditions to ensure the existence of nonnegative solutions for the state equation, the existence of optimal controls, and we develop the associated first order necessary optimality conditions. Finally, numerical simulations show the effectiveness of the proposed control strategy.
14:50 – 15:30
Palestrante: Marcelo Goulart Teixeira, Departamento de Ciências da Computação, Universidade Federal do Rio de Janeiro, Brasil
Título: Um novo modelo constitutivo para a cortiça
Resumo: A cortiça é um material natural utilizado pelo homem há mais de 5000 anos, normalmente em aplicações de natureza doméstica. Seu uso mais comum, como rolha para garrafas de vinho, data do início do século XVII e deve-se ao monge beneditino Dom Perignon. Porém, nos últimos anos, devido a características tais como baixa densidade, boa elasticidade, boa recuperação a ações compressivas e uma quase total impermeabilidade, além de excelente isolamento térmico, acústico e vibrático, a cortiça tem sido usada em um vasto campo de aplicações, nomeadamente em construção civil, nas indústrias naval e aeroespacial e na manufatura de equipamentos de segurança. Considerada um material hiperelástico, a cortiça é o único sólido que não sofre dilatação lateral. Dessa forma, a simulação numérica de problemas de grande deformação envolvendo a cortiça possui dificuldades interessantes do ponto de vista numérico. Nesta palestra vamos mostrar algumas propriedades mecânicas da cortiça, discutir as dificuldades de sua modelagem e apresentar um novo modelo constitutivo para este material. Será abordado também o método ALI (Aproximação Linear Incremental), um método Lagrangeano-Euleriano atualizado linearizado, e sua utilização na simulação de dois problemas clássicos de grande deformação envolvendo a cortiça.



